mat52

毎週水曜日定期発行
Weekly Mathematics Magazine

《数学通信》
MAT-52　1993.6.23(Wed)

★数学の迷信＜其の２＞★～数学は完成された学問？～

数学にまつわる迷信の二番手は，何と言ってもこれだ．

数学は完成された学問である．

日本人はどうもこう信じているようだ．なぜだろうか？断言してあげよう！絶対にそんなことはないんだぞ！！

我々が，君達がそう信じているのは，それは小学校以来ただひたすらに計算問題や，応用問題など，体系的に完成された部分だけを勉強させられてきたからだ．しかも，強制的に，暗記を強いられ，間違いを責められ，自由な発想をいっさい拒否されて．そんな感じで算数，数学を１０年間勉強させられてきたからだ．そんな中で数学を学んだのだから，数学が面白いと感じるのは，日本人のほんの一握りの人間にすぎないのも仕方がない話である．

それでも，大学の数学科に入れば，数学を大局的に見つめるチャンスに恵まれ，数学がまだまだ発展途上の学問である事に気がつく，きっと気がつくだろう．もちろん，数学科に入ったすべてが気がつくわけではないのだが．

しかし，それを体験できるのはまさに数万人に一人かも知れない．

間違えてはいけない．君達が学んでいる数学が数学の全てではないのだ．いや，むしろ，数学の世界への入り口を通過するためのパスポートを申請しているのだと思った方がいいだろう．今学んでいることが理解できれば，数学の世界への入場を許可されるのである．それから初めて，数学というものを学べるのである．そう考えた方がむしろ正解だといえよう．

現在，世界中の各分野の，もちろん数学における各分野であるが，第一人者と呼ばれる人々が，そしてそれらの人を師と仰ぐ人々が数学の発展にその全身全霊を傾けている．そのことは，君達が，我々がただ単に知らないだけである．知ろうとしていないだけなのである．

それは宇宙の膨張と似ている．

宇宙が膨張していようとしていなかろうと，我々の今日の暮らしには関係ない．数学が発展していようが完成していようが，スーパーでの買い物に困るわけではない．だからどうでもいいのである．数学に興味のない者にとっては，嫌いな数学になんか関心すら持ちたくない．それが正直なところであろう．

でも，現実を認識することは大切なことであるし，正しく理解することによって今までと異なる新しい発見，新しい感動が胸の中に巻き起こるかもしれないのである．そして，そのことがもとになって今まで嫌いであった数学が好きになるかもしれないではないか！！！

そう，まさに数学は宇宙と同じに現在膨張を続けているのだ．

そこで，数学の拡張の代表的な例を一つ話しておこう．

君達は中学生の時に，平面図形（三角形の合同や，平行四辺形など）や立体図形（三角錐や球など）を学習したと思うが，君達が学習した幾何（現在学習している幾何も）は，Ｅｕｃｌｉｄ（ユークリッド）幾何と呼ばれるものだ．

Ｅｕｃｌｉｄ幾何学は，紀元前３００年頃，ギリシャのＥｕｃｌｉｄのよって完成された幾何学で，それまでの数々の研究，例えばターレスやピタゴラスの諸定理，ソクラテスの証明法，プラトンの定義，ユードクロスの比例の理論などを集大成したものと言われている．

このＥｕｃｌｉｄ幾何学は定義，公準，公理，そして定理によって厳密に理論的に体系づけられたものだ．全部で１３巻あり，例えば，第１巻では，２４の定義，図形に関する５の公理，数量に関する８の公理，４８の定理からできている．

その中で，ここでは，図形に関する５の公理を紹介しておこう．公理とは証明無しで認められるもっとも基本的な命題を言う．

公理１任意の点と他の任意の点とを結ぶ直線を引くことができる．

公理２任意の直線はいかほどでも延長することができる．

公理３任意の点を中心とし，任意の半径で円をえがくことができる．

公理４直角は全て等しい．

公理５１平面上において１直線が２直線と交わり，その１直線の同じ側にある２つの内角の和が，２直角よりも小さいとき，この２直線をどこまでも延長すれば，２直線は和が２直角よりも小さい内角のある側で交わる．

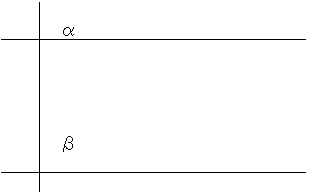
以上が”原本”の公理である．ここで，公理５が他の公理に比べて大変複雑であることに気がつくだろう．（公理１から公理４までは当たり前のことで，わざわざ言わなくてもと君達は思うことだろう．）

この公理５は現代の平行線の公理《１直線外の１点を通ってその直線に平行な直線は１つあって１つに限る．》と同じ命題である．

このＥｕｃｌｉｄの幾何学が出版？されてから今日に至るまでに，多くの数学者がこの公理５に疑問を持ち，チャレンジし続けてきた．そして，１９世紀はじめ，《直線外の１点を通ってこれと平行な直線が２本引ける．》という，一見奇妙な仮定をしてもＥｕｃｌｉｄ幾何学に似た別の幾何学が立派にできることが，ガウス，ロバチェフスキー，ボヤイの３人によって独立に発見された．これを，【非Ｅｕｃｌｉｄ幾何学】という．

この発見をとても大きな発見で，これを機に，数学は爆発的に進歩を遂げた．君達にはまだまだ解らないことがたくさんあるだろうが，ガウス等の偉大な発見は，それまでカオスの状態だった数学にビッグバーンを引き起こさせたことになる．

現代でも数学は広がり続けている．位相幾何やら，解析幾何，リーマン幾何など，Ｅｕｃｌｉｄを離れた幾何学が花盛りの状態といっても言い．

数学はただ単に計算をする事ではない．出来上がった問題の解法を暗記する学問でもない．条件を自ら揃え，自らの世界を作り上げていく，築き上げていく，まさに創造的な学問である．

いいかい，絶対に思い違いをしないで欲しい．受験の数学が本当の数学の姿ではないのだ！受験の数学は足切りの手段として，選別の手だてとして歪められた姿でしかない．もちろんだからといって，そんな数学ならやらなければいいではないか！？という，自分勝手な理屈が成り立つわけでもない．

現実を見なさい，現実を．正しかろうが，正しくなかろうが，乗り越えなければならない壁というものがあるんだよ．俗に言う，

『仕方がない．』である．

数学は完成された学問である．

そんなことはない！

今現在，数学は限りなく，果てしなく，膨張を続けている．今現在，数学は限りなく，果てしなく，膨張を続けている．

新しい数学の誕生はまさに君達の世代にかかっている．君達の若き柔軟な思考にかかっている．つまらない迷信などにまどわされる必要はない．思いのままに，自由で奇抜な，そして，ここが大切なのであるが，尚かつ論理的に，いいかい論理的に構築された数学の新しい世界の開発に努めて欲しい．

いかに発想が良くても，論理的に構築する力がないのでは，それでは数学にならない．

興味と，そして勇気のある者は，Let's Challenge!!!

Printed in Tounn.1993.
Written by Y.O^kouchi.1993.
Copyright 1987,1993 MAT Inc.
MAT is Mathematics Assist Team Corporation.