| 枅廡悈梛擔掕婜敪峴 Weekly Mathematics Magazine |  | 乻悢妛捠怣乼
MAT-60丂1993.9.29(Wed) |
![]()
仛柍尷傪尒偮傔傞丏仛乣Part3柍尷偺晄巚媍乣
壓偺嶰妏宍偺恾傪尒偰傎偟偄丏
嶰妏宍ABC偼惓嶰妏宍丏
奺曈偺拞揰傪D,E,F偲偟丆DE,FE傪寢傇丏
摨偠傛偆偵丆嶰妏宍DBF偵偮偄偰傕奺曈偺拞揰傪G,H,I偲偟丆GH,HI傪寢傇丏
埲壓摨條偺嶌嬈傪懕偗偰偄偒丄嵍恾偺傛偆側嶰妏宍傪昤偔丏
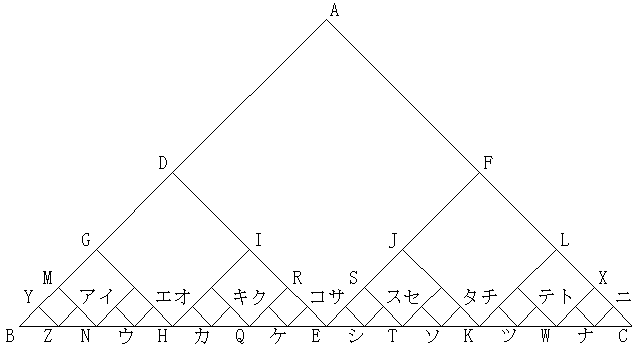
偄傑丆B偐傜A傪捠傝C傊峴偔摴偺傝傪峫偊傞丏偙傟傪B乣A乣C偲昞偡丏
D,E,F偼奺曈偺拞揰偱偁傞偐傜丆AD=DE,AF=FE丅廬偭偰B乣A乣C偼丆B乣D乣E乣F乣C偲偟偰傕摨偠偱偁傞丏乮佹AB=2DB=DB+DE,AC=2FC=FE+FC乯
摨偠傛偆偵峫偊偰偄偔偲丆師偺傛偆偵側傞丏
B乣A乣C亖B乣D乣E乣F乣C
亖B乣G乣H乣I乣E乣J乣K乣L乣C
亖B乣M乣N乣O乣H乣P乣Q乣R乣E乣S乣T乣U乣K乣V乣W乣X乣C
亖B乣Y乣Z乣傾乣N乣僀乣僂乣僄乣H乣僆乣僇乣僉乣Q乣僋乣働乣僐乣E乣僒乣僔乣僗乣T乣僙乣僜乣僞乣K乣僠乣僣乣僥乣W乣僩乣僫乣僯乣C
亖乧乧
![]()
偝偰丆偙偺嶌嬈傪塱墦偵懕偗偰偄偔偲偳偆側傞偩傠偆偐丠
BA+AC=BC偲側傞傛偆偵尒偊傞傛偹丏
偩偭偰丆柍尷偵忋偺恾偺嶌恾傪孞傝曉偟偰偄偔偺偱偁傞丏嵟屻偵偼丆彂偒偒傟側偔側傞偩傠偆偟丆B乣A乣C偼BC偵廳側傞丏
偲偄偆偙偲偼丆侾曈偺挿偝傪a偲偡傞偲丆
2a=a(a亗0)偲偄偆偍偐偟側幃偑惉傝棫偮偙偲偵側傞丏
僂乣儞偙傟偼偳偆愢柧偟偨傜偄偄偺偩傠偆丠
偪傚偭偲峫偊偰傒偰傎偟偄丏偙偺偁偨傝偺撪梕偼丆棃擭偺亀旝暘丒愊暘亁偺妛廗撪梕偵偮側偑偭偰偄偔偲偙傠偱偁傞偐傜丆俛僐乕僗偺幰偼摿偵僱丏
柍尷傪峫偊偰偄偔偲丆偄傠偄傠偲晄巚媍側偙偲丆偍偐偟側偙偲偑偱偰偔傞丏忋偺椺傕偦偺堦偮偱偁傞丏
偮偄偱偵傕偆堦偮丏
帺慠悢偺廤崌傪峫偊傞丏偙偺廤崌偺拞枴偲偟偰偼丆
1,2,3,4,5,6,7,8,9,10,丒丒丒偲偄偭偨傕偺偑嬶懱揑偵偁偘傜傟傞偑丆偦偺屄悢偼丠偲暦偐傟傞偲丆乽柍尷屄乿乧嘆偲摎偊偞傞傪摼側偄丏偦傝傖偦偆偩丏帺慠悢偵偼廔傢傝偑側偄丏柍尷偵偮側偑偭偰偄傞偺偱偁傞丏偩偐傜屄悢傕柍尷屄偱偁傞丏偦傟偼惓偟偄丏
偱偼丆師偵丆惍悢偺廤崌傪峫偊傞丏偙偺廤崌偺拞枴偼丆
偲偁偘傜傟丆傗偭傁傝丆偦偺屄悢偼偲暦偐傟傟偽丆乽柍尷屄乿乧嘇偲摎偊偞傞傪摼側偄丏
摨條偵丆桳棟悢偺廤崌傪峫偊傞丏丒丒丒-2,丒丒丒,-併2,丒丒丒,1,丒丒丒,併3,丒丒丒偺條偵昞偡偙偲偑偱偒丆屄悢偼傗偭傁傝乽柍尷屄乿乧嘊偱偁傞丏
偝偰丆偙偙偱栤戣偱偁傞丏
嘆丆嘇丆嘊偺屄悢偼丆偳傟傕柍尷屄偱偁傞丏偱偼丆偳偺柍尷屄偲偄偆戝偒偝傕摨偠側偺偩傠偆偐丠偦傟偲傕丆嘆偺柍尷屄偲丆嘇偺柍尷屄偲偱偼丆摨偠傛偆偵柍尷屄偲撉傫偱偄傞偑丆偦偺屄悢偵堘偄偼偁傞偺偩傠偆偐丠
扨弮偵峫偊傟偽丆嘆偺柍尷屄偼乣巒傑偭偰丆惓偺曽岦傊偺柍尷偱偁傞丏偦傟偵懳偟偰丆嘇偺柍尷屄偼傪婎弨偵偟偰丆嵍塃傊偺柍尷偱偁傞丏屄悢偲偟偰偼丆嘇偺曽偑嘆偺俀攞+1偩偗偺屄悢偑偁傞傛偆偵巚偊傞丏
偑丆尰幚偼偦傟傎偳娙扨偱偼側偄丏
乽柍尷乿偲偼悢偊愗傟側偄亖悢偊傜傟側偄丆偲偄偆奣擮偱偁傞丏悢偊愗傟側偄丆悢偊傜傟側偄傕偺偵懳偟偰丆悢偊傜傟傞傕偺偺屄悢偺奣擮傪帩偪崬傫偩偲偙傠偱丆偦偺奣擮偑捠梡偡傞偲偄偆曐忈傕側偄丏
偩偐傜偦傫側偵娙扨偵俀攞偁傞丆偲偼尵偊側偄偺偱偁傞丏偙偺偁偨傝偺奣擮偼擄偟偄丏偦傟偙偦偐側傝偺棟榑峔抸傪偟側偗傟偽偄偗側偄偟丆暲偺棟夝椡偱偼棟夝偟擄偄丏
偑丆偙傟偩偗偼尵偭偰偍偙偆丏
柍尷偵傕丆彫偝側柍尷偲丆戝偒側柍尷偑偁傞偺偱偁傞丏偙傫側偙偲傪尵偆偲丆傑偨傢偐傜側偔側傞偐側丠偨偩偟丆偩偐傜偲偄偭偰嘆偺俀攞偑嘇偲偄偆偙偲偱偼側偄丏
偑丆嘆偑堦斣彫偝側柍尷偺廤崌偱偁傞偙偲偵娫堘偄偼側偄丏
墢偑偁傟偽丆婡夛偑偁傟偽丆傑偨柍尷偺榖偟傪偟傛偆丏乣廔乣
![]()
 |
Printed in Tounn.1993.
Written by Y.O^kouchi.1993. Copyright 1987,1993 MAT Inc. MAT is Mathematics Assist Team Corporation. |