解答2

（１）△ＡＢＣの外側に正方形ＢＦＧＣ、ＣＨＩＡ、ＡＤＥＢを解答欄に書き込め。

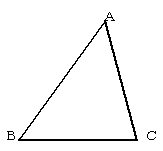
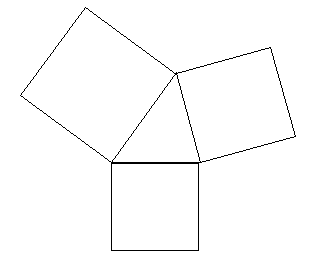
（２）ＢＩ＝ＣＤで、ＢＩ⊥ＣＤであることを証明せよ。

この3つの正方形の中心を順に、Ｏ₁，Ｏ₂，Ｏ₃とおく。
（３）辺ＢＣの中点Ｍを利用して、Ｏ₁Ｏ₂＝CＯ₃で、Ｏ₁Ｏ₂⊥CＯ₃であることを証明せよ。

線分ＦＩの中点をＮとする。
（４）ＡＯ₃＝ＡＮ，ＡＯ₃⊥ＡＮであることを証明せよ。

回転と相似を上手利用できるかがポイント。

（１）

　（２）△ＡＤＣと△ＡＢＩを考える。
　　　ＡＤ＝ＡＢ、ＡＣ＝ＡＩ
　∠ＤＡＣ＝９０°＋∠ＢＡＣ＝∠ＢＡＩ　だから
　　　　△ＡＤＣ≡△ＡＢＩ
　よって、ＢＩ＝ＤＣ
　また、△ＡＤＣをＡを中心に９０度回転すると△ＡＢＩに重なるから、
　　　　　ＢＩ⊥ＤＣ　　（証明終わり）

　（３）△ＭＯ₁Ｏ₂と△ＭＣＯ₃においてＭＯ₁=ＭＣ
　　　
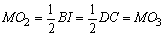
　　　ＭＯ₂ / / ＢＩ，ＭＯ₃ / / ＤＣより　ＭＯ₂⊥ＭＯ₃
　よって、△ＭＯ₁Ｏ₂をＭを中心に９０度回転して、Ｏ₁をＣに重ねると、Ｏ₂はＯ₃に重ならなければならない。
　故に、Ｏ₁Ｏ₂=ＣＯ₃，Ｏ₁Ｏ₂=ＣＯ₃　（証明終わり）

　（４）△ＡＯ₃Ｃと△ＡＮＩにおいて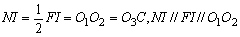だから
　　　ＮＩ⊥O₃Ｃ，ＡＣ＝ＡＩ
　よって△ＡＯ₃ＣをＡを中心に９０度回転して、ＣをＩに重ねると、Ｏ₃はＮに重ならなければならない。
　故に、ＡＯ₃=ＡＮ，ＡＯ₃⊥ＡＮ　（証明終わり）