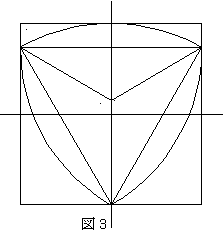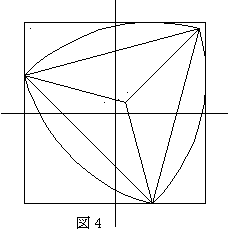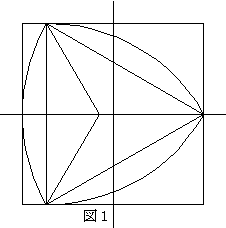
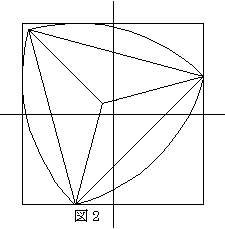
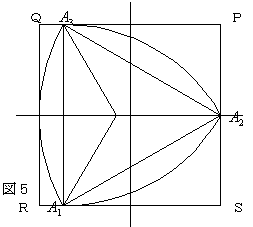今、図１、図２、図３、図４の様に１辺の長さが２の正方形の内部を、ル−ロ−の三角形が反時計方向に回転するものとする。

問１
右図５の様にP１，１），Ｑ（−１，１），Ｒ(−１，−１)，Ｓ（１，−１）なる正方形ＰＱＲＳの内部に、ル−ロ―三角形 Ａ₁Ａ₂Ａ₃が存在する時、点Ａ₁，Ａ₂，Ａ₃の重心Ｇの座標を求めよ。

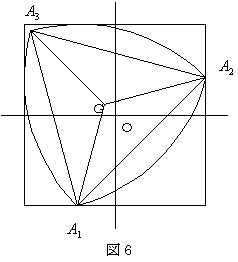　右図６の様に、ル−ロ−の三角形が、正方形ＰＱＲＳの内部を、反時計に回転する時

問２
３０度回転した時の点Ａ₁，Ａ₂，Ａ₃，重心Ｇの座標を求めよ。

問３
更に、３０度回転した時の点Ａ₁，Ａ₂，Ａ₃，重心Ｇの座標を求めよ。

問４
ル−ロ−の三角形が、正方形の中で完全に1回転した時、重心Ｇが原点Ｏを中心に、円周のような道のまわりを何回、回転するか。

問５
以下同様に、正方形の内部を反時計まわりに回転する時、ｔ°(0≦ｔ≦30°)回転した時の重心Ｇのｘ座標、ｙ座標をｔを使って表せ。ただし、点Ｖ（ｘ，ｙ）を原点Ｏを中心にθ度回転した点をＷ（Ｘ，Ｙ）とすると、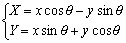となる。

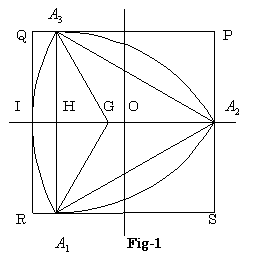　Ｐ（１，１），Ｑ（−１，１），Ｒ（−１，−１），Ｓ（１，−１）より
右図より
　　Ａ₂Ａ₃＝２，Ａ₃Ｈ＝１，ＨＡ₂＝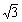
　　ＩＨ＝ＩＡ₂−ＨＡ₂
　　　　∴　ＩＨ＝２−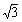
ＩＨ＋ＨＯ＝１よりＨＯ＝１−(２−)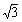
　　　　∴　ＨＯ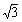＝−１
座標で表示すると
　　Ａ₁＝(１−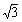，−１)，Ａ₃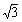＝(１−，１)
Ｇは重心だから、ＨＧ：ＧＡ₂＝１：２
　　ＧＡ₂＝２ＨＧ
ＧのＸ成分をＸ_Gとすると
　　１−Ｘ_G＝２｛Ｘ_G−(１−)｝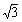
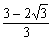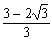　　　∴　Ｘ_G＝，Ｇ(，０)
これらをまとめると
　　Ａ₁(１−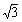，−１)，Ａ₂(１，０)，Ａ₃(１−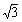，１)，Ｇ(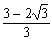，０)

問２

Ｓｔｅｐ１
　ル−ロ−の三角形Ａ₁Ａ₂Ａ₃を重心Ｇを中心に、反時計方向に３０度回転した点Ａ₁'，Ａ₂'，Ａ₃'の座標を求める。
Ａ₂(１，０)，Ｇ(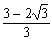，０)より
　　ＧＡ₂＝１−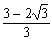　　　∴　ＧＡ₂＝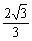
Ａ₂をＧ(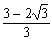，０)を中心に、30度回転するとFig-2のようになる。
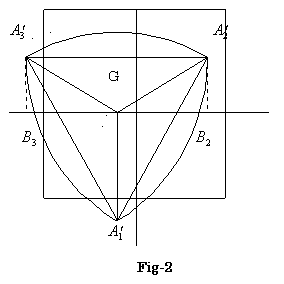Ａ₂'からＸ軸へ垂線を下ろし、Ｘ軸との交点をＢ₂とする。
　　ＧＢ₂＝ＧＡ'₂cos30°
　　ＧＢ₂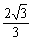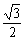＝×＝１
ＧＯ＋ＯＢ₂＝ＧＢ₂より
　　ＯＢ₂＝ＧＢ₂−ＧＯ
　　ＯＢ₂＝１＋＝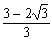
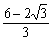
Ｙ成分について考えると
　　Ａ₂'Ｂ₂＝ＧＡ₂'sin30°＝＝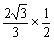
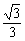
　　　∴　Ａ₂'(，)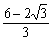
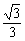以下同様に、Ａ₃'を求めると
Ａ₃'からＸ軸へ垂線を下ろし、Ｘ軸との交点をＢ₃とおくと
　　Ｂ₃Ｇ＝ＧＡ₃'cos30°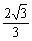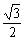＝×＝１
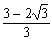　　ＯＢ₃＝−１＝−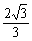
Ｙ成分について考えると、
　　Ａ₃'Ｂ₃＝ＧＡ₃'sin30°＝×＝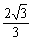

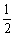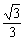
Ｓｔｅｐ2
　Fig-2のままでは、正方形からはみだしてしまうので、正方形のなかにすっぽりと収納されるように、ル−ロ−の三角形を平行移動しなければいけない。
　Ａ₂'がｘ＝1に接する様に、Ａ₁'がｙ＝−１に接するように、つまりｘ軸方向へ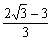、ｙ軸方向へ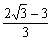平行移動するとFig-3　　のような図になる。
　Ａ₁'，Ａ₂'，Ａ₃'をｘ軸方向へ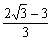、ｙ軸方向へ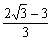平行移動した点をＡ₁''，Ａ₂''，Ａ₃''とおくと、

平行移動前
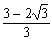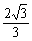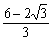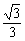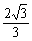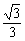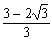　Ａ₁ '(，−)，Ａ₂' (，)，Ａ₃' (−，)，Ｇ(，０)

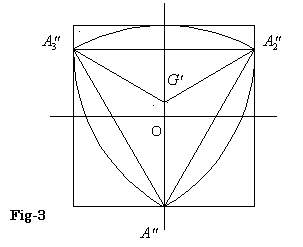
平行移動後
　
　
　
　

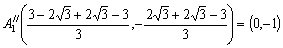
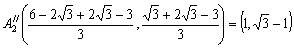
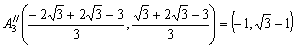
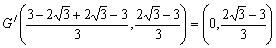
問3
　　初期条件　　　30度回転　　　60度回転
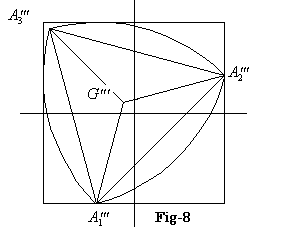
　更に30度回転すると、Fig-4の状態になるので、過去の規則性から
　　Ａ₃''' (−１，０)，Ａ₁ ''' (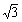−１，−１)，Ａ₂''' (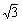−１，１)， G''(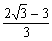，０)
となる。

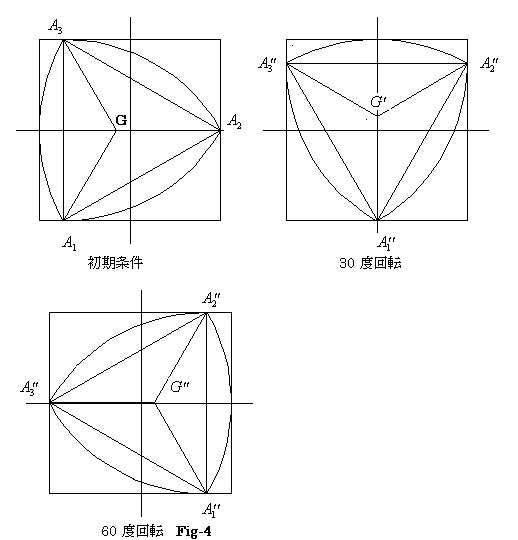
問4

　初期状態Ａ₂(１，０)が、反時計方向に30度回転した時、重心Ｇは逆方向つまり時計方向へ−90度回転しＧ'へ移動することがわかる。

　つまり、Ａ₂が完全に１回転した時、重心Gは３回転することになる。

問5

　重心Gの軌跡の方程式についてル−ロ―の三角形が回転角ｔ(０≦ｔ≦３０)の時、重心Gの軌跡の方程式を求める。

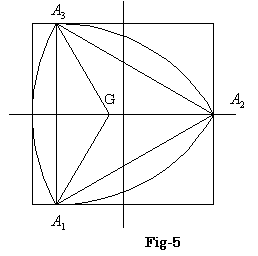
初期条件
　Ａ₁(１−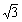，−１)，Ａ₂(１，０)，Ａ₃(１−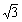，１)，Ｇ(１−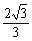，０)
Ｓｔｅｐ　１
　ル−ロ−の三角形の重心Ｇと、Ｏが一致する様に平行移動し、更にＯを中心に反時計方向にｔ(０≦ｔ≦３０)回転した時のＡ₁'，Ａ₂'，Ａ₃'を求める。

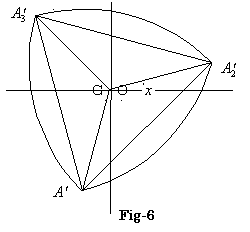
　Fig-5のル−ロ−の三角形の重心ＧをＯに一致する様に平行移動したときのＡ₁，Ａ₂，Ａ₃をＡ₁⁰，Ａ₂⁰，Ａ₃⁰とおく。
　　Ａ₁⁰(−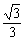，−１)，Ａ₂⁰(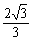，０)，Ａ₃⁰(−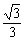，−１)
　つまり、ｘ軸方向に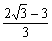だけ、平行移動した。
Ａ₁⁰，Ａ₂⁰，Ａ₃⁰をＯを中心にｔ(０≦ｔ≦３０)反時計方向に回転した点をＡ₁'，Ａ₂'，Ａ₃'とおくと。回転角の公式を利用して
　　，，
　　
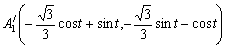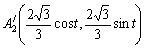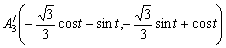
この３点 Ａ₁'，Ａ₂'，Ａ₃'をFig-5の重心Ｇの点、元の重心座標に戻してみると、正方形からはみだしてしまうが、Fig-7のようになる。
　つまり、ｘ軸方向へ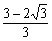平行移動すると
　　，
　　
　　

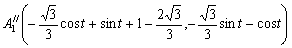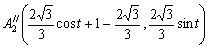
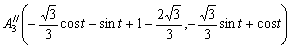
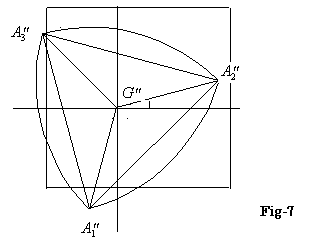
　次に、Fig-7のル−ロ−の三角形を正方形の中へ戻すための平行移動を考える。

ｘ成分について
　Ａ₂''が直線ｘ＝1に接する様に平行移動する。つまり、ｘ軸方向へ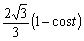平行移動する。
ｙ成分について
　Ａ₁''が直線ｙ＝−1に接する様に平行移動する。つまり、ｙ軸方向へ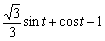平行移動する。
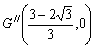　は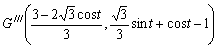に平行移動される。
　重心Ｇの軌跡の方程式は、ｔをパラメ−タ―として
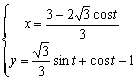　　　(０≦ｔ≦３０)
と表示される。

　 ［発展］

　この軌跡の方程式は、いったいどのような形状をしているのだろうか？
　『Mathematica』という数式処理ソフトで作図してみた。Ｇの軌跡は恐らく円になるだろうと予想していたのですが…。
　Fig-9が０≦ｔ≦３０の時、Fig-10が０≦ｔ≦３６０の時で作図したものです。

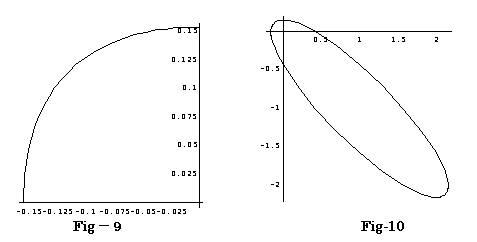
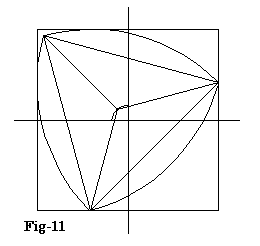
見て理解できるように、重心G　　の軌跡のは、楕円の一部であって、円ではなかった。 問3の解答の図Fig-4をみれば理解できる様に、３０度の回転でＧは９０度回転する。つまり、Fig-9のような形をした楕円の一部を、４つ貼り合わせた形になる。
　Fig-11になる。
　実生活では、ル−ロ−の三角形の形をしたドリルの刃を回転させて、正方形の穴をあけたりすることは、良く知られているのだが、重心Ｇがいったいどのような動きをするのかは、以外に知られていない。
　その他にル−ロ−の５角形で。正６角形の穴を作成することもできるようです。
　このような問題を「変心ドリル問題」と呼んでいるようです。
　興味・関心がある生徒は、この他にもどんな穴が作成可能なのか、いろいろと考えてみると、面白いと思います。