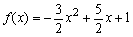解答4

　２次関数

は、ｆ(ａ)＝ｂ，ｆ(ｂ)＝ｃ，ｆ(ｃ)＝ａ（ａ，ｂ，ｃは整数）を満たしている、次の各問いに答えよ。

（１）ａ≠ｂ，ｂ≠ｃ，ｃ≠ａを示せ。

（２）{ｘ｜ｆ(ｘ)＞ｘ}∩｛ａ，ｂ，ｃ｝≠φを示せ。

（３）ａ，ｂ，ｃを求めよ。

（１）ａ，ｂ，ｃが整数であることが重要。
（２）ａ，ｂ，ｃの中の最大数に着目せよ。
（３）（２）の条件を満たす整数を探す。

（１）ｆ(x)＝ｘを解くと
　　３ｘ²－５ｘ－２＝－２ｘ
　　３ｘ²－３ｘ－２＝０
　　　∴　

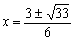（整数ではない。）
　よってａ＝ｂ，ｂ＝ｃ，ｃ＝ａのいずれも起こらない。

（２）ａ，ｂ，ｃは異なる３つの整数だから、今、ａが最大の数ならば、ｆ(ｃ)＝ａより
　　　　ｆ(ｃ)＞ｃ
　となり、｛ｘ|ｆ(ｘ)＞ｘ｝にｃは属する。
　他も同様に、最大数に対して、ｆ(ｘ)＞ｘを満たすものが存在する。　　（証明終わり）

（３）ｆ(ｘ)＞ｘを解くと
　　３ｘ²－３ｘ－２＜０
　　
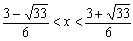
　これを満たす整数はｘ＝０，１に限る。
　ｆ(０)＝１，ｆ(１)＝２，ｆ(２)＝０だから、
　　　(ａ，ｂ，ｃ)＝(0，1，2)，(1，2，0)，(2，0，1)
　の３組である。