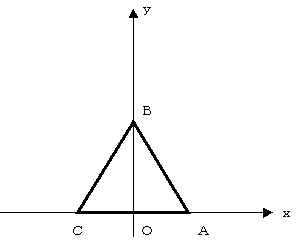
（１）Ｏから辺ＡＢに達し、さらに辺ＢＣで反射し、３回目でＯに戻るとき、角θを求めよ。

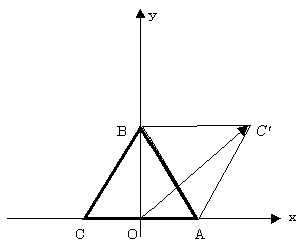
（２）辺ＡＢで反射し、１回目で頂点Ｃで止まるとき、tanθの値を求めよ。

（３）Ｏから各辺で２回反射し、ある頂点で止まるとき、tanθの値を求めよ。

（４）Ｏから各辺で５回反射し、ある頂点で止まるとき、経路が最も長くなる場合は、どの頂点に達するときで、その経路の長さはいくらか。

（５）Ｏから各辺で偶数回反射し、ある頂点に達する経路は、ただ1つであることを説明せよ。

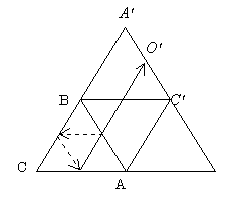
２）Ａ(１，０)，Ｂ(０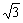，)，Ｃ'(２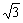，)だから

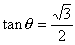
（3）２回反射して頂点に達するのは、ＯＡ'の経路に限る。
　　Ａ'(１，２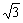，)だから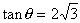　

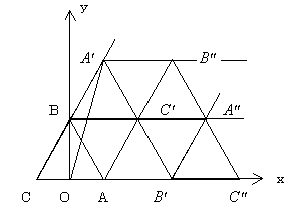
（4）５回反射して頂点に達するのは、図の３経路ある。
　　Ａ'''(４，３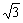)，Ｃ'''（５，２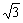），Ｂ'''(６，)
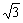だから、経路が最も長いのは、頂点Ａに達する時で、長さは、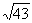

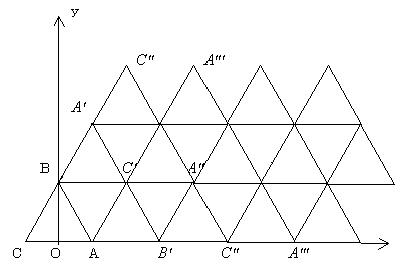
（５）（４）の図において、
　　△ＡＢＣの内部の点は、反射しないで達し得る。
　　△ＡＢＣ'の内部の点は、反射１回で達し得る。
　　△Ａ'ＢＣ'，△ＡＢ'Ｃ'の内部の点は、反射２回で達し得る。
　今、偶数回反射して達し得る三角形内部の点の領域に斜線を施すと、△ＡＢＣから始まり、互にうろこ模様を作る。
　辺ＣＢの延長上にある頂点以外は、奇数回反射して達する頂点からなるので、偶数回反射して到着する頂点は、Ａ'，Ｃ''，Ｂ'''，・・・の順にあり、Ａ'は２回、Ｃ''は４回、Ｂ'''は６回反射というように、２回ずつ反射が増えていく。