第18回北海道高等学校数学コンテスト　問題

問　　　題

平成12年1月11日(火)
9時00分～12時30分(210分)実施

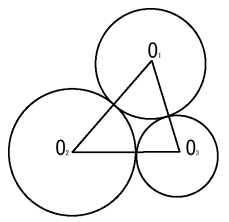
問題1

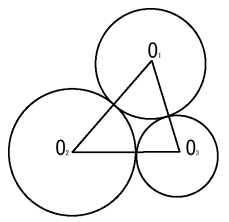
右図のように3つの円が外接している。この円の中心および半径をそれぞれＯ₁，Ｏ₂，Ｏ₃およびｒ₁，ｒ₂，ｒ₃とする。また，円Ｏ₂，Ｏ₃の接点をＰ，円Ｏ₁，Ｏ₃の接点をＱ，円Ｏ₁，Ｏ₂の接点をＲとする。
　次の問いに答えよ。

(1)△Ｏ₁Ｏ₂Ｏ₃の内接円は，3点Ｐ，Ｑ，Ｒを通ることを示せ。
（考察過程で用いた図も解答用紙に書くこと）

(2) △Ｏ₁Ｏ₂Ｏ₃において∠Ｏ₁Ｏ₂Ｏ₃＝θとするとき，cosθをｒ₁，ｒ₂，ｒ₃を用いて表せ。

(3) △Ｏ₁Ｏ₂Ｏ₃の外接円の半径Ｒをｒ₁，ｒ₂，ｒ₃を用いて表せ。

問題2

右図は，線分ＡＢを直径とする円で，Ｐは円周上の点である。

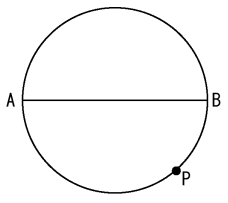
(1) 直径ＡＢの上側の半円周の中点Ｃを作図せよ。

(2) 線分の長さに関する関係式
　　　AP・BC＋AC・BP＝AB・CP
が成り立つことを証明せよ。

(3) 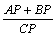の値を求めよ。

問題3

ａ，ｂ，ｃ，ｄは互いに等しくない自然数である。

(1) 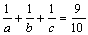を満たすａ，ｂ，ｃを求めよ。

(2) 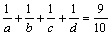を満たすａ，ｂ，ｃ，ｄを求めよ。

問題4

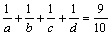座標平面上の原点にウサギが一匹いる。ウサギは1秒ごとに四方の格子点のいずれかに移動する。ただし，移動可能な４点へは各々

の確率で移動するものとする。
（注）ここで格子点とは，点(ｘ，ｙ)ｘ，ｙがともに整数であるものである。
（例）ウサギの位置が，点(1，1)のとき，1秒後には(1，0)，(0，1)，(1，2)，(2，1)のいずれかに移動する。
このとき，次の各問いに答えよ。

(1)2秒後にウサギが移動可能な格子点をすべて表示し，各々の格子点に移動する確率を求めよ。

(2)3秒後にウサギが直線ｙ＝ｘ＋ｋ（－３≦ｋ≦３，ｋは整数）上の格子点に移動する確率をの値ごとに求めよ。

(3)ｎ秒後にウサギが直線ｙ＝ｘ＋ｋ（－３≦ｋ≦３，ｋは整数）上の格子点に移動する確率を推測して求めよ。

問題5

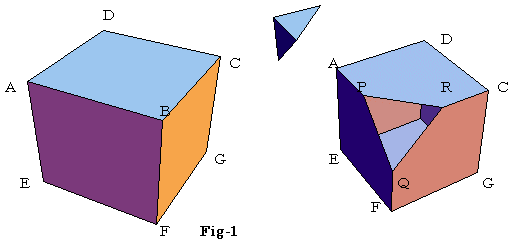
　下図Fig-1の様に，１辺が３の立方体ＡＢＣＤＥ－ＥＦＧＨが存在する。この立方体の頂点Ｂから，各頂点Ａ，Ｆ，Ｃへ向かって，同じ一定の速さで３点Ｐ，Ｑ，Ｒが動くものとする。

問１　このFig-1の立方体ＡＢＣＤＥ－ＥＦＧＨを平面ＰＱＲで切断する時，ＰＢ＝ＱＢ＝ＲＢ＝ｘとして，断面積ＰＱＲをｘで表せ。

問２　０＜ｘ＜３　の範囲で横軸をｘ，断面積ＰＱＲを縦軸とするグラフを作成せよ。

　右図Fig-2の様に立方体の各辺を３等分してできる中央部分の直方体をくり抜いた立体を作成する。

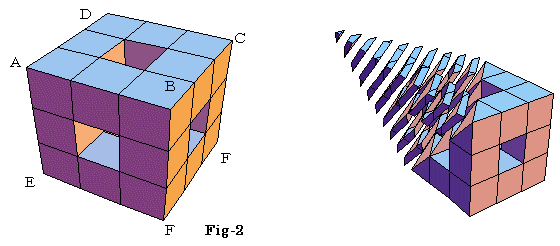
問３　Fig-2を平面ＡＣＦで切断したときの断面図を作図せよ。

問４　Fig-2の立体において，ＰＢ＝ＱＢ＝ＲＢ＝ｘとして断面積ＰＱＲをｘで表し，０＜ｘ＜３の範囲でグラフを作成せよ。

　更にFig-3の様に立方体の各辺を９等分してできる中央部分の直方体を取り除いた立体を作成する。

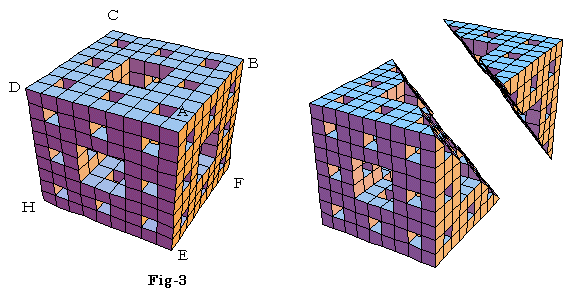
問５　ＰＢ＝ＱＢ＝ＲＢ＝ｘとして断面積ＰＱＲをｘで表し，０＜ｘ＜２の範囲でグラフを作成せよ。