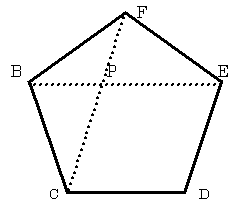
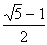 栤侾
栤侾仮俛俠俥偲仮俹俥俛偑憡帡偱偁傞帠傪棙梡偡傞丅
俠俥丗俛俥亖俛俥丗俹俥丂丂俠俥亖倶偲偍偔
倶丗侾亖侾丗倶亅侾
倶2亅倶亅侾亖侽
夝偺岞幃傪梡偄偰
丂丂丂
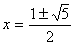
倶亜侽傛傝丂丂
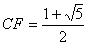
 栤俀
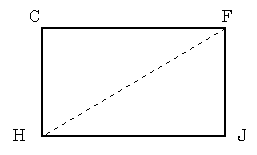
栤俀慄暘俥俫傪媮傔傞
丂丂丂俠俫亖俥俰亖侾丂丂
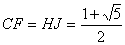
僺僞僑儔僗偺掕棟傪梡偄偰
丂丂丂
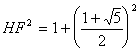
丂丂丂
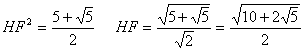
栤俁
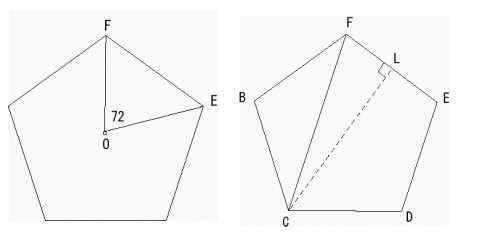
惓屲妏宍偺拞怱傪俷偲偡傞丅
惓屲妏宍俛俠俢俤俥偺奜愙墌偺敿宎俼傪媮傔傞丅
仮俷俤俥偵偍偄偰梋尫掕棟傪棙梡偡傞丅
丂丂俤俥2亖俷俥2亄俷俤2亅俀俷俥丒俷俤丒cos72亱
丂丂侾亖俼2亄俼2亅俀俼2cos72亱
丂丂侾亖俀俼2(侾亅cos72亱)丂 乧嘆
cos72亱偺抣傪媮傔傞丅揰俠偐傜曈俤俥傊悅慄傪偍傠偟揰俴偲偡傞丅
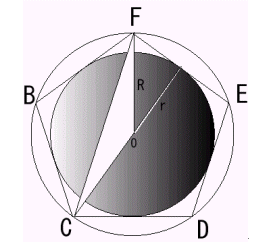 丂丂丂
丂丂丂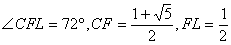
丂丂丂
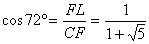 丂 乧嘇
丂 乧嘇嘇傪嘆傊戙擖偟偰
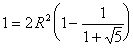 傛傝
傛傝丂丂丂
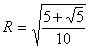
惓屲妏宍俛俠俢俤俥偺撪愙墌偺敿宎倰傪媮傔傞丅
丂丂丂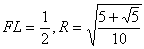
傛傝僺僞僑儔僗偺掕棟 倰2亄俥俴2亖俼2傛傝
丂丂丂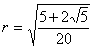
偙偺棫懱偺崅偝倛傪媮傔傞丅
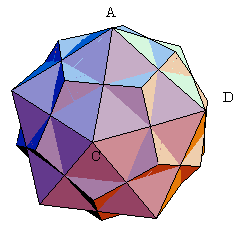
壓恾偺棫懱偵偍偄偰丄揰俠偐傜掙柺傪娷傓暯柺傊悅慄傪壓傠偟丄偦偺揰傪俹偲偍偔丅
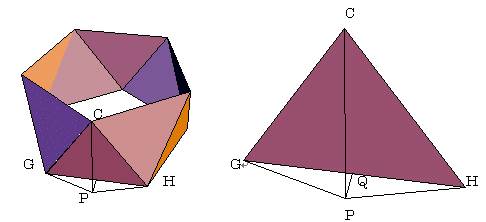
慄暘俧俫偺拞揰傪俻偲偍偔丅
丂丂丂
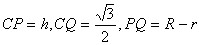
仮俠俹俻偼捈妏嶰妏宍丂僺僞僑儔僗偺掕棟傛傝
丂丂丂
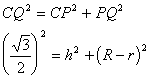
丂丂丂
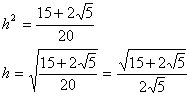
栤係
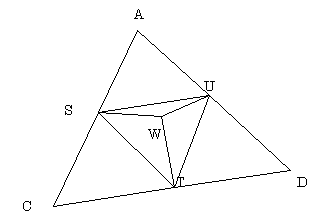
惓擇廫柺懱忋偺1偮偺柺仮俙俠俢偵偍偗傞惓廫擇柺懱偺捀揰倂偲偍偔
丂丂丂俽倂亖俿倂亖倀倂亖倶
丂丂丂俽俿亖俿倀亖倀俽亖侾/俀
丂丂丂俙俠亖俠俢亖俢俙亖侾
仮俽倂俿偵偍偄偰梋尫掕棟傪揔梡偡傞丅
丂丂丂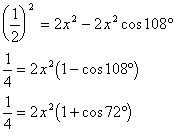
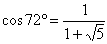 傪戙擖偟偰丄
傪戙擖偟偰丄
丂丂丂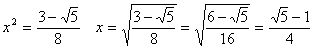
廬偭偰丄惓廫擇柺懱偺1曈偺挿偝偼丄