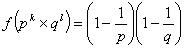従って、ｆ(８)＝４/８＝１/２
１から１０８までの自然数の中で、１０８と互いに素である数は、
１，５，７，１１，１３，１７，１９，２３，２５，２９，３１，３５，３７，４１，４３，４７，４９，
５３，５５，５９，６１，６５，６７，７１，７３，７７，７９，８３，８５，８９，９１，９５，９７，
１０１，１０３，１０７
である。従って求める確率は ｆ(１０８)＝３６/１０８＝１/３
または、次のように求めてもよい。１０８＝２2３3 より、
２の倍数は １０８/２＝５４（個）、３の倍数は １０８/３＝３６（個）、６の倍数は １０８/６＝１８（個）
１０８と互いに素である数は １０８−(５４＋３６−１８）＝３６ ｆ(１０８)＝３６/１０８＝１/３
同様にして、２００１＝３×２３×２９ より
３の倍数は ２００１/３＝６６７（個）、２３の倍数は ２００１/２３＝８７（個）、２９の倍数は ２００１/２９＝２３（個）
６９の倍数は ２００１/２９＝２９（個）、２３×２９ の倍数は ２００１/(２３×２９)＝３（個）、３×２９ の倍数は ２００１/(３×２９)（個）、３×２９×２３ の倍数は ２００１/(３×２９×２３)＝１（個）
以上から、２００１と互いに素な整数は、２００１−（６６７＋８７＋６９−２９−３−２３＋１）＝１２３２（個）
従ってｆ(２００１)＝１２３２/２００１
（２）ｎ＝ｐk より １，２，３，…，ｐ，ｐ＋１，ｐ＋２，…，２ｐ，２ｐ＋１，…，ｐkの中で、ｐk と互いに素である数とは、ｐで割り切れない数のことである。ｐの倍数は、ｐk-1 個あるので、ｐk と互いに素な整数は、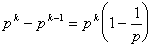
個存在する。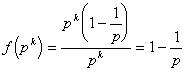 
（３） ｎ＝ｐkｑl（ｐ，ｑ は異なる素数、ｋ，ｌ≧１ ）のとき、１，２，３，…，ｐkｑl の中で、ｎと互いに素でない数は、ｐの倍数またはｑの倍数である。
ｐの倍数はｐ番目ごとにあるのでｎ/ｐ個ある。ｑ の倍数はｑ番目ごとにあるのでｎ/ｑ個ある。
同様に、ｐｑの倍数はｎ/ｐｑ個あるので、１，２，３，…，ｐkｑl の中で、ｎと互いに素な数は、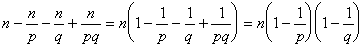
個存在する。
従って 