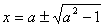 よって、
よって、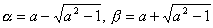
解と係数の関係より αβ=1
(2)α2=A とおく
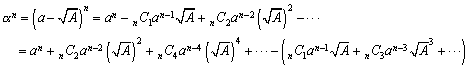
同様に 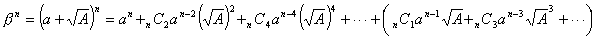
ゆえに 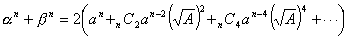
よって αn+βn は偶数となる。
(3)(2)より αn+βn=2T (T:整数)とおく。
βn=2T-αn=2T-1+(1-αn)
ここで、0<α<β,αβ=1 より 0<α<1,0<αn<1
ゆえに 0<1-αn<1
βn の整数部分mは2T-1となり、奇数である。
(4)βn=m+s …①
(3)より s=1-αn αn=1-s …②
ここで αnβn=(αβ)n=1
βn=1/αn
①②より m+s=1/(1-s)
よって m=1/(1-s)-s