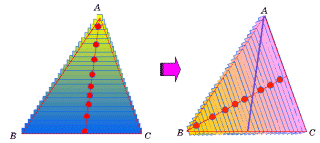
三角形の幾何的重心は次のように求めることもできる。三角形をひとつの底辺に平行にスライスして短冊の形に千切りする。その各々の短冊の重心は中点であることから、その短冊の重心を集めてできる線分(中線)上に、もとの三角形の重心は乗っている。この千切りを他の辺についても試みると、中線の交点が重心ということになる。
このように図形を一定間隔の短冊にスライスすると、そのおのおのの短冊の重心を質点とする加重平均がもとの図形の重心となる。このことを利用して、閉曲線で囲まれた図形の重心を求めてみよう。
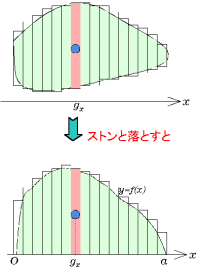デカルト座標上の図形を鉛直方向に等間隔にスライスし、長方形状の短冊を作る。次にこの図形をx軸上に落とすと、図のように図形はx軸上に乗る。この短冊の上限の値を結んでできる曲線の方程式をy=f(x)とすると、f(x)とx軸および区間0≦x≦aで囲まれる図形の重心のx座標は、元の図形の重心のx座標と一致する。(カヴァリエリの原理)。
そこで、この図形の幾何的重心のx成分を gx とし、その回りのmomentを考えると、
∴
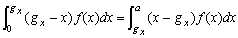
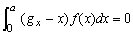
これは点 gx の回りの回転力が０であることを示している。これから、
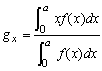
が得られる。同様にy軸方向の重心の位置も計算できる。
では、幾つかの図形の重心を実際に求めてみよう。