２．変身を表す一次変換

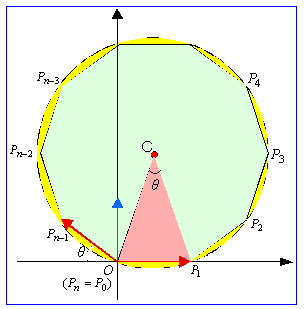
　新図へ変身させるには、正多角形の１頂点を挟む２辺のなす角を直角に変換すればよい。
　正ｎ角形P₁P₂P₃……P_n-2P_n-1P_nをP(n)と表現する(ただし、P₀=P_nとする)。
　P(n)の外接円の中心Cに対して、θ＝∠P_kCP_k+1をP(n)の中心角とよぶことにする。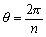で与えられるが、n=3，4の場合の新図は明らかなので、n≧5でとすると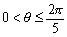となりθは鋭角と考えてよい。
　次に、P₀(0，0)，P₁(1，0)に固定し、基底となる正多角形の二辺をP₀P_n-1，P₀P₁とする。すなわち、一辺の長さ１の正多角形を考えることになる。ここで、
　　　
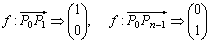
なる変換ｆを表す行列Tを求めてみよう。

　∠P_n-1P₀P₁＝π−θより、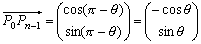
　　　
である。よって、
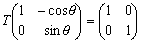　　　　より、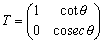
この一次変換f：Ｔにより、新世界への道が開かれる。
　ところで、
　　　
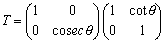
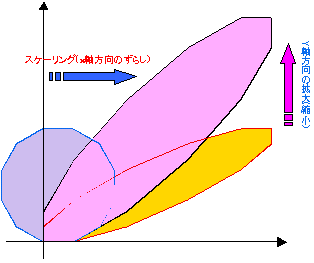
であるから、一次変換ｆは、x軸方向へずらし変換をした後、y軸方向へcosecθ倍する変換であることがわかる。
　では、新世界ｆのgateであるこの行列を通過すると図形はどのように変換されるから調べてみよう。