|
Nature1 P(n)の外接円の中心をCとするとき、一次変換fにより ① 直線OCは、直線y=xに移される。 ② 直線OCの法線は、直線y=xの法線に移される。 |
OPn-1=OP1=1，∠Pn-1OC=∠COP1より①は明らかである。同様に原点を通る法線は、∠Pn-1OX-∞の二等分線であることより②も明らかであるが、具体的に計算してみよう。
外接円の中心の座標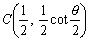
をfで移す。
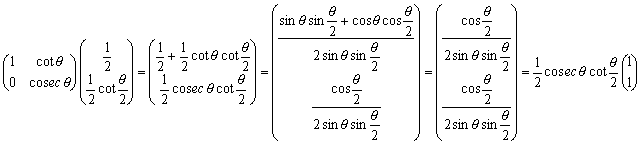
また、法線の方向ベクトルは、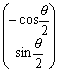
であることより、
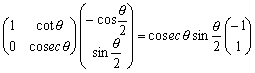となる。
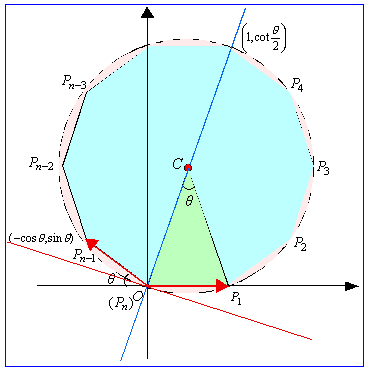
以上、Nature1の①,②より次の結果を得る。
|
Nature2 P(n)の外接円に外接する原点を通る正方形は、fにより長方形に移される。 |
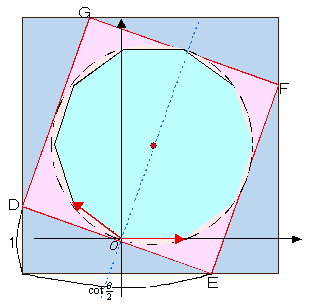
右図の正方形の変換である。では、この正方形をfで移してできる長方形の二辺の長さを求めてみよう。
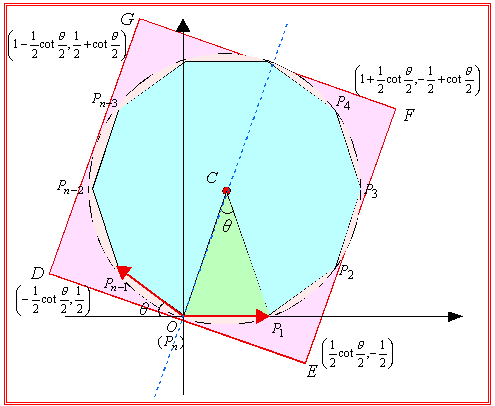
まず、元図の正方形の各頂点ＤＥＦＧを図のようにとり、その座標を求める。
頂点Ｄは、円の中心Cを原点の回りに90°回転した点であるから、
∴ 
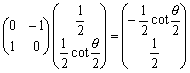
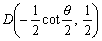
また、頂点Aを原点に関して対称移動すると、
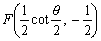
である。
次に、線分ＤC，ＥCをそれぞれ２：１の比に外分した点が頂点Ｆ，Ｇであるから、
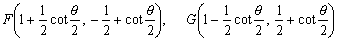
となる。
結果、右図のようなuniqueな図ができあがる。
さて、ではこの正方形ABCDをfにより変換した長方形の２辺ａ，ｂ(ａ＞ｂ)の長さを求めてみよう。
まず、外接円の直径が長方形の1辺の長さａに対応することから、
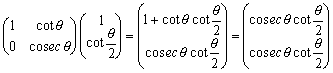
よって、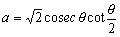
である。
また、点Aをfで移して、
∴ 
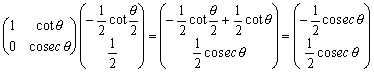
である。
以上より
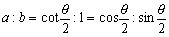
となる。
|
Nature3 P(n)の外接円は、直線ｙ＝ｘ上に長軸がある原点を通る楕円に移される。 |
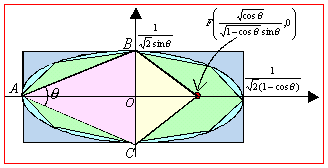P(n)の外接円は、Nature2の正方形の内接円であるから、fによる変換によって、長方形に内接する楕円に移されることは明らかである。なお、長軸と短軸の長さの比は
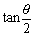である。
その楕円の概形であるが、右図の楕円をx軸方向に、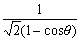
平行移動し、原点の回りに45°回転したものであり、方程式は、
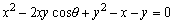
となる(証明略)。
ところで右図において、
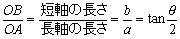
より、∠BAC＝θである。
すなわち、元円の直径を弦とする円周角(90°)はfによってθに変換される。
以上、Nature1～Nature3より、次の結論を得る。
|
Nature4 P(n)はfにより、頂点f(Pk)と頂点f(Pn-k)が直線y=xに関して対称なn角形に移される。 |
P(n)において、直線PkPn-kはOCの法線であるからNature1より新図においてはy=xの法線となる。かつ、y=xは楕円の長軸でありことよりNature4が示される。