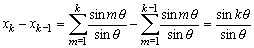これが本稿の主テーマであるが、結論をいうと、
| 作図可能なP(n)のfによる像もまた作図可能である。 |
ということになる。その証明のための準備を少ししよう。
|
Nature5 x軸上の点はすべて不動点である。(y=0は不動直線である) |
x軸上の点を(k,0)とすると、
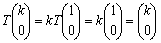
より明らかである。なお、y=0以外の不動直線についても調べておこう。
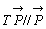 であればよいから、
であればよいから、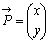 とおくと、
とおくと、
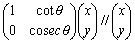
より、(x+cotθ・y)y=cosecθ・yx、(xsinθ+ycosθ)y=xy
∴ 不動直線は、 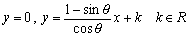
ここで、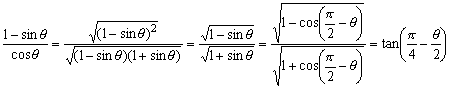
であるから、x軸の正の方向となす角が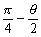 である直線が不動直線である。
である直線が不動直線である。
|
Nature6 直線群 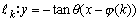 は、fにより、直線群 は、fにより、直線群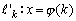 に変換される。 に変換される。
|
これは、一次変換fが、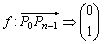 であることと、x軸上の点が不動点であることから分かる。
であることと、x軸上の点が不動点であることから分かる。
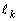 のベクトル方程式は、
のベクトル方程式は、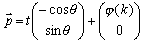 であるから、
であるから、
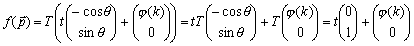
このNature6から、新世界におけるy座標軸が確定する。一次変換fは、x軸方向のずらしを表す変換であったが、この変換の特徴は同じ傾きのものを同じ角度だけずらすということである。表現行列Tの場合は、その角度は90°−θである。
imageとしては、この変換は次のように捉えればよいだろう。
原図のP(n)はもちろんx-y直交座標上の図形であり、それがfによる斜交座標上の新図に変換される。これを、もともとの図形をx軸と直線P0Pn-1を軸とする斜交座標とみれば、相対的にはfにより直交座標へ変換されることになる。ただ、新図においては軸の目盛間隔が、一定ではない(ある意味では一定だが)。よって、目盛幅をplotできれば、新世界における新図の作図ができることになる。
それをNature6の性質が可能にする。
では実際に作図をしてみよう。
|
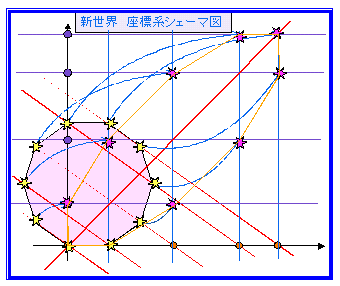
以上の操作で新世界における新図が完成する。
ただ、これだけでは単に描けるというだけで、実際の問題への応用はできない。
そこで次にこの新世界での目盛幅の規則性を考えてみよう。
|
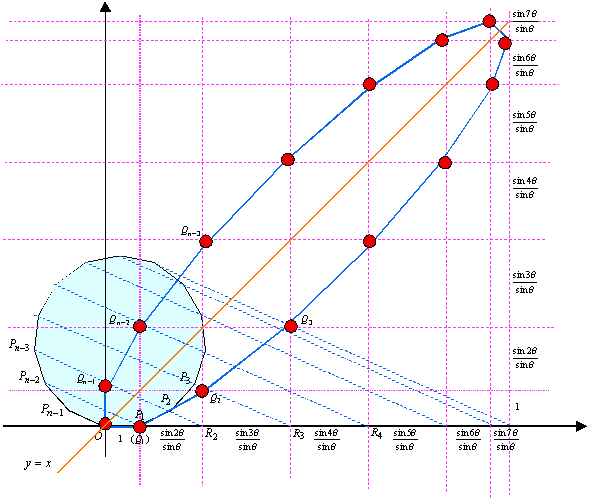
Nature7 新座標軸の目盛を 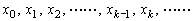 とすると、 とすると、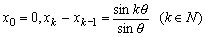 である。 である。
|
まず、Pkの座標を求めよう。
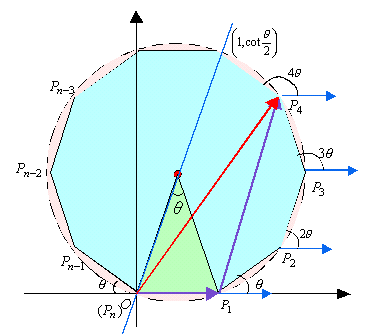
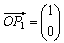 より、
より、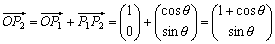 となる。
となる。
以下、同様に
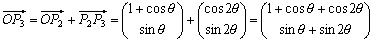
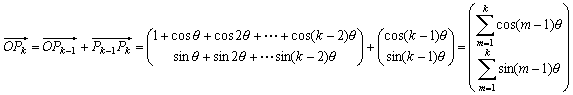
これより、直線PkPn-k-1の方程式は、 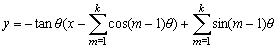
よって、x軸との交点Rk(xk,0)
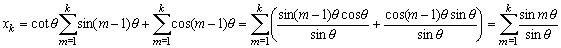
以上より、