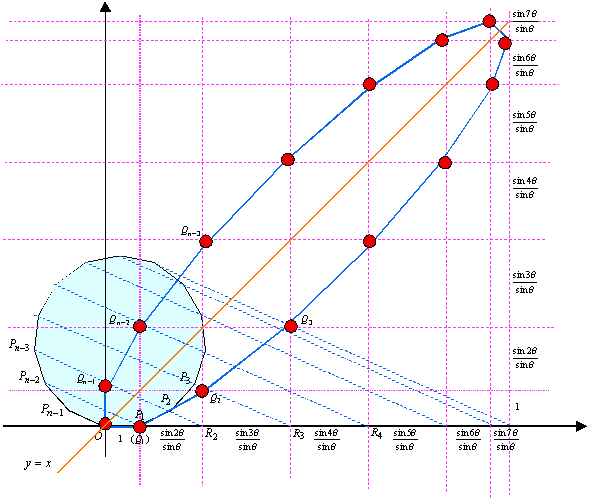
この新世界の座標系の一番の特徴は、直線y=xに関して、頂点が対称に配されるということである。これは、x軸とy軸の目盛幅を同じ間隔に取ることにより、新世界において座標の擬似正規化をしたためである。しかし、このことにより元図から新図への変換過程が少し複雑なものになってしまった。もう少し、simpleでslimな変身ができないか次に考えてみる。
一次変換を表す行列で、このｙ軸の目盛間隔の正規化に関与したのは、y軸方向の拡大(縮小)変換を表す表現行列
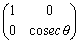………(*)である。この行列を通過せずにせん断を表す一次変換
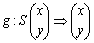
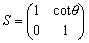
P(n)を移してみよう。
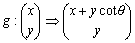
であるから、y座標は不変でx座標だけがｙcotθ分傾くことになる。この一次変換の像を新たな新世界とすると元世界との対比が容易である。変換fでは、本来はx,y座標ともに基底が変換されるため、新図を描こうとすると新たに座標を作らなければならない。元図の中に書き込むことには無理があるのである。しかし、変換gはスライドするだけであるから元図の中に混在させることが可能である。変換gの性質を次に示す。
- 直線OCの像は直線ｙ＝sinθ･ｘである。
- 新図ではy軸の目盛間隔は、x軸の間隔のsinθ倍である。
- 一次変換gは等面積変換である。
(1),(2)は、拡大縮小変換(*)の性質を考えれば明らかである。(3)は、
det(S)=1
となることから分かる(なお、fでは、det(T)=cosecθより、面積は、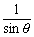
倍であった)。
これらの性質は、受験問題の解法などでは元図では見え難い背景を新図で考えることにより、思考そのものもslim化できるのである。この座標系で描いたP(n)の新世界を巻末に載せたのでごらんいただきたい。
