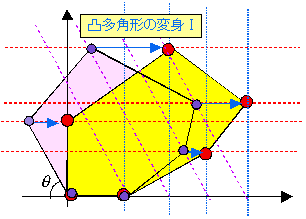
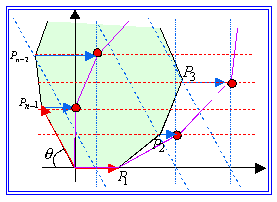
これまで正多角形P(n)の変身を考えてきたが、スケーリングのずらし変換はどんな図形に対しても実際は可能である。正多角形のように、容姿端麗である必要はない。だれだって新世界へのキップはもっている。
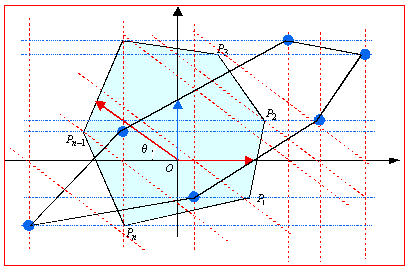
問題は、何を新世界の基底として考えるかである。一次変換gの働きをみると、変換に関わっていたのは、P(n)の二辺OP1とOPn-1である。OP1をx軸上にとり単位ベクトルとすることで、OPn-1をy軸上に移せばよかっただけで、正多角形P(n)の中心角θに対して表現行列Ｓを確定する必要はないのである。したがって一般の多角形P1P2……Pn-1Pnについても、θ=∠Pn-1OX-∞とし、このθに対して、一次変換
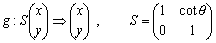
を考えればよい。あとは、OPn-1に平行で各頂点を通る直線とx軸との交点を新世界での目盛幅として設定していく。 このように考えるとどんな多角形でも新世界にtripできるのである。
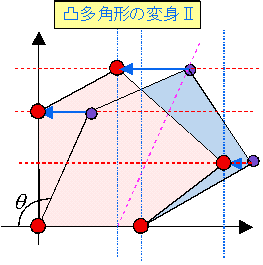
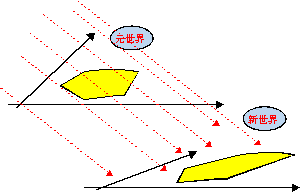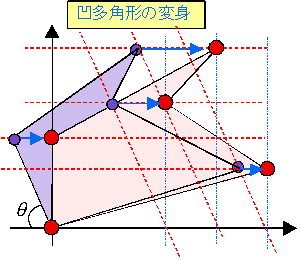
実は、二辺を基底と考える必要すらない。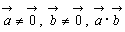
のとき、この2つのベクトルを基底として平面が作られるわけであるから、平面上に適当に置かれた図形に対して、適当に基底を決めれば上記の手順から変身多角形が作られることになる。ただ、どう変換しても多角形の高さ（ｙ座標の目盛間隔）は変わることはない。x軸方向にスライドするだけである。すなわち、ずらしの度合いが、θの設定によって微妙に変化していく。例えれば、太陽光が、刻々と変化して我々の世界に射し込むときにできる影のように、ある平面世界に光が射すとき、その平面に平行な平面世界に映る影が変身多角形なのである。
