新教育課程3年間の実践から
新教育課程3年間の実践から
1994（平成6)年度から新しい教育課程になって，今年度で3年目を迎えました。担任かつ教科担任として，とまどいいながらもいろいろと実践してきました。今は新課程3年目の総仕上げということで進路指導も最後の追い込みに入っています。今回のレポートは，3年間の実践を振り返って「生徒にとって興味関心のあった教材について」まとめてみました。
1年生は全員必修で「数Ⅰ」は4単位，「数A」は1単位。
6年度から新教育課程になり，目標・内容・進度・評価について数学科で研修の必要性を確認し，教科内で研修に取り組む。
「数A」･･･数と式・恒等式（5月中旬頃迄）
「数Ⅰ」について
旧課程と違って第1章 2次関数，第2章 方程式・不等式となっており，授業展開でやや戸惑うことがあった。2次関数の決定は計算力不足の生徒にとって難しく感じられたようである。連立方程式で時間のかかる生徒も少なくない。また，応用問題で式の作れない生徒も目立つt。関数から方程式へ･･･という流れは，生徒にとって戸惑いがあったようである。
第3章 三角比，第4章 個数の処理，第5章 場合の数については，全般的に生徒はよく学習に取り組み理解できたようである。
3学期は第6章 確率を終えてから「数A」の「数列」に入る。等差・等比数列に力を入れる。シグマのところは1年生にとっては難しい内容であるが，生徒はよくがんばり学習に励んでいた。
「数Ⅱ」について（3単位）
第1章 図形と方程式，第2章 三角関数（1学期まで）
1学期は予定より遅れてしまうが，ヤムをえない。生徒の授業態度は良好であった。不等式と領域には十分時間をかけれなかった。
2学期は加法定理・指数関数・対数関数までしか進まず。
授業中は私語も無く集中して学習していて大変よい。
3学期は第4章 微分法，第5章 積分法の定積分まで終える。
「数B」について（3単位）
第1章 複素数と複素数平面(1学期)の「複素数平面」は，生徒にとっては難しく感じたかもしれない。数B（選択）の生徒は，3年生では理科コースを希望しているのがほとんどの為，意欲的に学習に取り組んでいた。
2学期は第2章 平面上のベクトル，第3章 空間のベクトルを実施。
数B選択の生徒は，数Ⅱの成績も大変良く，授業にも真剣に取り組み教科担任もやりがいがあった。ベクトルについては生徒の方が，こちらの予想以上にわかってくれた，
3学期は第4章 確率と分布（確率変数の期待値まで終えた）。
生徒にとっては，教科書・問題集がやさしすぎる為自主教材を作成した。
「数Ⅲ，数C」について（4+2単位）
理科コースのため必修である。生徒は興味・関心を持って授業に真剣に取り組み意欲的に学習している。
生徒にとってウルトラＣでも興味・関心のある教材について
y=｜x+2｜+｜x－1｜+｜x+3｜のグラフを書け。
y=f(x)=｜x2－1｜+｜x－1｜について，次の問いに答えよ。
(1) y＝f(x)のグラフを書き，－2≦x≦2における最大値を求めよ。
(2) aを正の数とする。－a≦x≦aにおけるy＝f(x)の最大値が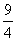
であるようなaの値の範囲を求めよ。
｜x｜+2｜y｜=1のとき，x2+y2の最大値と最小値を求めよ。
x≧0のとき，xの小数第1位を4捨5入して得られる整数をm(x)とし，xを越えない最大の整数を[x]とする。
y=m(x)とy=[x]のグラフを比較することにより，記号[]を用いてm(x)を表せ。
x2－(2－a)x+1+a=0について，次の問いに答えよ。
(1) 1つの解が0<x<2の範囲にあり他の解がx<0または2<xの範囲にあるように，定数aのとり得る値の範囲を定めよ。
(2) 相異なる2つの解のうち少なくとも1つが0<x<2の範囲にあるように定数aのとり得る値の範囲を定めよ。
(3) a<－1のとき，解xのとり得る値の範囲を求めよ。
2次方程式x2+ax+b=0の2つの解をα，βとする。α，βが2次の2つの条件0≦α2+β2≦4，0≦α+β≦1を同時にみたすように，整数(a,b)の組を定めよ。
不等式x2-(a-1)x+a-2<0･･･(ｱ)，2x2-3x-2>0･･･(ｲ)がある。このとき，次の問いに答えよ。
(1) 不等式(ｱ)に解があるためのaの値の範囲を求めよ。
(2) 不等式(ｱ)，(ｲ)を同時にみたすxの値が存在するようなaの値の範囲を求めよ。
問1．放物線C：y=x2+k と直線l：y=kx-3がある。このときCとlの共有点が2<x<3と3<x<4の範囲に1つずつ存在するようにkの値の範囲を定めよ。
問2．f(x)=x2-(k+1)x+k-2がx≦0のとき，つねにf(x)>0であるための定数kの値の範囲を求めよ。
問1．△ABCにおいて，頂点Aの座標は(2，16)，重心の座標は(3，-1)，外心の座標は(2，1)であるとき，頂点B，Cの座標を求めよ。ただし，頂点Bのx座標は，正の値とする。
問2．O(0，0)，A(5，2)，B(x，y)を頂点とする△OABの垂心の座標がH(3，1)であるとする。このときB(x，y)を求めよ。
問3．3点O(0，0)，A(1，0)，C(0，3)を頂点とする△OACの面積が点B(3，0)を通る直線で2等分されるとき，この直線の方程式を求めよ。
問1．複素数平面上に正方形ABCDがある。対角線ACとBDの交点をEとするとき，線分EAをEを中心として正の向きに90°まわすとEBとなり，さらに正の向きに90°まわすとECとなる。このときA，Bを表す複素数をそれぞれα，βとする。C，D，Eをα，βを用いて表せ。
問2．2点(p，q)，(-q，p)を結ぶ線分を1辺とする正方形の中心の座標を求めよ。
問1．y=x-2sin x (0≦x≦2π)
問2．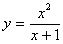
問3．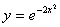
問4．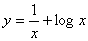
0<x<1では1<1+x2<1+xである。これを用いて，不等式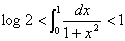
を証明せよ。
楕円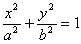
は，媒介変数を用いてx=acosθ，y=bsinθ(0≦θ≦2π)と表される。このことを使って，この楕円で囲まれる部分の面積を求めよ。ただしa>b>0とする。
円x2+(y-2)2=1をx軸の周りに1回転してできる立体の体積を求めよ。