今一直線上で向きが同じベクトルの集合をEとする。Eの中の任意の に対してa
に対してa を対応させる変換
を対応させる変換
fa; ├→a
├→a
を考える。ここでaは正の実数であるがこのような変換faは倍変換と呼び
a; ├→a
├→a
と表してもよい。
今後はこの変換を実数aを特徴づける変換と考えることにするのである。従って変換に関する諸 性質を前提として実数aに関する諸性質を導き出すことが可能である。
だが次のような疑問もあり得る。ベクトル に対してベクトルa
に対してベクトルa を対応させる変換という場合のa
を対応させる変換という場合のa とは実数aを前提としてa
とは実数aを前提としてa が定義されている。しかるに、変換
が定義されている。しかるに、変換 ├→a
├→a をもって実数aを特徴づけるという事は可能ではあるが、根本的には循環論になってしまうのではないのか。
をもって実数aを特徴づけるという事は可能ではあるが、根本的には循環論になってしまうのではないのか。
このような疑間はもっともな事であり、変換の諸性質を前提として数の性質を導く場合、いきな
り変換から実数を導くという訳にはいかないのである。ユークリッド式量の検討から始めてユーク
リッド式量空間の公理系の設定へと進む。そこから倍概念の検討を経て、量空間の倍変換として自
然数、有理数、実数へと数の定義とそれに基づく諸性質が導かれてゆくのである。しかし、ここで
はその過程について触れると議論があまりにも長大になるので割愛したのであるが、要するに変
換;x├→a によって実数aと定義することは循環論におちいる事なく理論展開が可能なのである。今述べた事を明確に論じた理論は南雲道夫博士の論文Quantities and Real Numbersに詳しく展開されている。
によって実数aと定義することは循環論におちいる事なく理論展開が可能なのである。今述べた事を明確に論じた理論は南雲道夫博士の論文Quantities and Real Numbersに詳しく展開されている。
またこの理論を受け継ぎ発展させたものとして、田村二郎先生の理論がある。これは対称量空間
の検討を経て、対称量空問における倍変換として負の実数を導き、更に2次元対称量空間の倍変換
として複素数を導くというものである。
(この理論は、田村二郎著「量と数の理論」(日本評論社)に詳しいが、残念ながらこの書は現在で
は絶版のようである。)
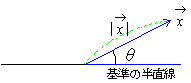 さて、ベクトルを表わすのに、そのペクトルの長さと、基準の半直線とのなす角を用いてみよう。
さて、ベクトルを表わすのに、そのペクトルの長さと、基準の半直線とのなす角を用いてみよう。
このとき =(|
=(| |、θ)と表わす。
|、θ)と表わす。
するとa>0として
a =(a|
=(a| |、θ)
|、θ)
となる。
 =(|
=(| |、θ1)
|、θ1) 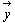 =(|
=(|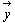 |、θ2)
|、θ2)
とすると
 =
=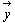 ならば、|
ならば、| |=|
|=|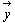 |、かつθ1=θ2+2nπ
|、かつθ1=θ2+2nπ
となる。
次に一直線上のベクトルの集合Sを考える。
任意の ∈Sに対して、その逆ベクトル
∈Sに対して、その逆ベクトル '∈Sが決まる。このとき変換
'∈Sが決まる。このとき変換 ;
; ├→
├→ 'を対称変換と呼ぷ。
'を対称変換と呼ぷ。
対称変換は ├→-
├→- となる変換であるから(-1);
となる変換であるから(-1); ├→-
├→- のように考えて、実数-1を特徴づける変換として考えることができる。
のように考えて、実数-1を特徴づける変換として考えることができる。
対称変換と対称変換の合成は恒等変換になる。
(-1); ├→
├→ ' 続いて(-1);
' 続いて(-1); '├→
'├→ ''
''
よって
(-1)・(-1); ├→
├→ ''
''
ところで ''=(
''=( ')'=
')'= であるから
であるから
(-1)・(-1); ├→
├→
となる。これは
1; ├→
├→
と同じ変換であるから
(-1)・(-1)=1
となる。
また集合Sにおいては実数倍変換と対称変換とは可換である。
2つの合成変換、
(-1)・a; ├→-(a
├→-(a ) a・(-1);
) a・(-1); ├→a(-
├→a(- )
)
において
-(a )=a(-
)=a(- )
)
を示そう。
 =(|
=(| |、θ)とする。
|、θ)とする。
a =(a|
=(a| |、θ) ∴-a
|、θ) ∴-a =(a|
=(a| |、θ+π)
|、θ+π)
また
- =(|
=(| |、θ+π)、a(-
|、θ+π)、a(- )=(a|
)=(a| |、θ+π)
|、θ+π)
となる。よって
a(- )=-(a
)=-(a )
)
となる。従って合成変換(-1)・aとa・-(-1)とは同じ合成変換となり
(-1)・a=a・(-1)
となる。
以上のようにある極の変換を考えることによって、その変換によって、特徴づけられる数を考え ることができ、更に変換の性質から数に関わる性質を導くことも出来るのである。