丂暋慺悢偼偳偺傛偆側曄姺偵傛偭偰摿挜偯偗傜傟傞偱偁傠偆偐丅
丂暋慺悢偺奣擮傪柧妋偵偡傞堊偵偼師偺俁偮偺帠暱偑杮幙揑側偙偲偱偁傞丅
- 嫊悢扨埵倝偲偼倝2亖亅侾傪枮偨偡丅偙偺傛偆側悢倝偲偼擛壗側傞曄姺偐傜摫偐傟傞偺偐丅
- 幚悢倐偲嫊悢扨埵倝偲偺愊偲偼偳偺傛偆側堄枴傪傕偮偺偐丅
- 倎偲倐倝偲偺榓偲偼壗傪堄枴偡傞偐乮扐偟倎丄倐偼幚悢)
丂偙偙偱暯柺儁僋僩儖偺廤崌倀傪峫偊傞丅 伕倀偵懳偟偰兾/俀夞揮堏摦偟偨儀僋僩儖傪
伕倀偵懳偟偰兾/俀夞揮堏摦偟偨儀僋僩儖傪 *伕倀偲偡傞丅
*伕倀偲偡傞丅
丂 亖(|
亖(| |丄兤)偲偡傞偲
|丄兤)偲偡傞偲 *亖(|
*亖(| |丄兤亄兾/俀)偲側傞丅
|丄兤亄兾/俀)偲側傞丅
丂偙偙偱師偺傛偆偵掕媊偡傞丅
乻掕媊乼
暯柺儀僋僩儖偺曄姺丗劌仺
*傪嫊悢扨埵傪摿挜偯偗傞曄姺偲屇傃倝偱昞傢偡丅
偡側傢偪丄倝丟劌仺
*
傑偨丂倝丟劌仺倝
偲偡傞偲
*亖倝
丄
偮傑傝曄姺倝偲偼暯柺儀僌僩儖傪兾/俀夞揮偝偣傞曄姺偱偁傞丅
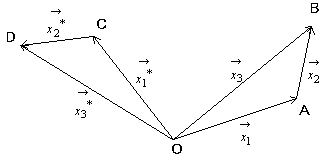 丂偙偺曄姺倝偼慄宆偱偁傞偙偲傪帵偦偆丅
丂偙偺曄姺倝偼慄宆偱偁傞偙偲傪帵偦偆丅
恾偱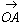 亖
亖 1丄
1丄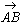 亖
亖 2丄
2丄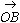 亖
亖 3偲偡傞丅
3偲偡傞丅
丂俷傪拞怱偲偡傞兾/俀夞揮偵傛偭偰丄揰俙丄揰俛偼丄偦傟偧傟揰俠丄揰俢偵堏傞偲偡傞丅偙偺偲偒
丂丂丂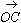 亖
亖 1*丄
1*丄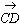 亖
亖 2*丄
2*丄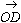 亖
亖 3*
3*
偲側傞丅
崱丄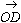 亖
亖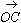 亄
亄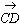 偵忋幃傪戙擖偟偰
偵忋幃傪戙擖偟偰
丂丂丂 3*亖
3*亖 1*亄
1*亄 2*丂丒丒丒嘆
2*丂丒丒丒嘆
丂偙偙偱
丂丂丂 3亖
3亖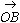 亖
亖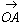 亄
亄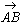 亖
亖 1亄
1亄 2丄
2丄
丂丂丂 1*亖倝
1*亖倝 1丄
1丄 2*亖倝
2*亖倝 2丄
2丄 3*亖倝
3*亖倝 3
3
傪嘆偵戙擖偡傞丅
丂丂丂倝 3亖倝(
3亖倝( 1亄
1亄 2)亖倝
2)亖倝 1亄倝
1亄倝 2
2
丂丂丂亪丏丂倝( 1亄
1亄 2)亖亖倝
2)亖亖倝 1亄倝
1亄倝 2
2
傛偭偰曄姺倝偼慄宆偱偁傞丅
丂師偵崌惉曄姺倝墏蓚聜膷l偊傞丅
丂丂丂倝丟 劌仺
劌仺 *丂懕偄偰丂倝丟
*丂懕偄偰丂倝丟 *劌仺(
*劌仺( *)*
*)*
傛偭偰倝墎G 劌仺(
劌仺( *)*偲側傞丅
*)*偲側傞丅
 亖(|
亖(| |丄兤)偲偡傞偲
|丄兤)偲偡傞偲
丂丂丂 *亖(|
*亖(| |丄兤亄兾/俀)丄
|丄兤亄兾/俀)丄
丂丂丂( *)*亖(|
*)*亖(| |丄兤亄兾/俀亄兾/俀)
|丄兤亄兾/俀亄兾/俀)
傛偭偰( *)*亖(|
*)*亖(| |丄兤亄兾)亖亅
|丄兤亄兾)亖亅
廬偭偰倝墎G 劌仺亅
劌仺亅 偲側傝偙偺曄姺偼(亅侾)丟
偲側傝偙偺曄姺偼(亅侾)丟 劌仺亅
劌仺亅 偲摨偠曄姺偱偁傞丅
偲摨偠曄姺偱偁傞丅
傛偭偰倝墎亖|侾丄崌惉曄姺倝墏茥獘L偡傞偙偲偵偡傟傁倝2亖亅侾偲側傞丅
丂懕偄偰倝偲幚悢倎偲偺愊偼壜姺偱偁傞偙偲傪帵偡丅
丂偙傟偼崌惉曄姺倝亗苽仴倝偲偑摨偠曄姺偱偁傞偙偲傪帵偡偙偲偵側傞丅
丂丂丂倎墎G 劌仺倎(倝
劌仺倎(倝 )
)
丂丂丂倝亖G 劌仺倝(倎
劌仺倝(倎 )
)
偱偁傞偐傜寢嬊偼倎(倝 )亖倝(倎
)亖倝(倎 )偲側傞偙偲傪妋偐傔傟偽傛偄偺偱偁傞丅
)偲側傞偙偲傪妋偐傔傟偽傛偄偺偱偁傞丅
倎亖侽偲 亖
亖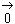 偺応崌偼帺柧側偺偱徣棯偟丄倎亗侽丄偦偟偰
偺応崌偼帺柧側偺偱徣棯偟丄倎亗侽丄偦偟偰 亖(|
亖(| |丄兤)偲偟偰峫偊傞丅
|丄兤)偲偟偰峫偊傞丅
(鶣)倎亜侽偺偲偒
 )亖倎(|
)亖倎(| 丄兤亄兾/俀)亖(倎|
丄兤亄兾/俀)亖(倎| |丄兤亄兾Q)
|丄兤亄兾Q)丂傑偨丄倝(倎
 )亖倝(倎|
)亖倝(倎| |丄兤)亖(倎|
|丄兤)亖(倎| |丄兤亄兾/俀)
|丄兤亄兾/俀)丂傛偭偰倎(倝
 )亖倝(倎
)亖倝(倎 )
)
(鶤)倎偔侽偺偲偒
丂丂丂倎(倝
 )亖亅倐(倝
)亖亅倐(倝 )亖亅倐(|
)亖亅倐(| |丄兤亄兾/俀)
|丄兤亄兾/俀)丂丂丂丂亖(倐|
 |丄兤亄兾/俀亄兾)
|丄兤亄兾/俀亄兾)丂丂丂丂亖(倐|
 |丄兤亄俁兾/俀)
|丄兤亄俁兾/俀)丂丂丂倝(倎
 )亖倝(亅倐
)亖倝(亅倐 )亖倝(倐
)亖倝(倐 ')亖倝(倐|
')亖倝(倐| |丄兤亄兾))
|丄兤亄兾))丂丂丂丂亖倝(倐|
 |丄兤亄兾)亖(倐|
|丄兤亄兾)亖(倐| |丄兤亄兾亄兾/俀)
|丄兤亄兾亄兾/俀)丂丂丂丂亖(倐|
 |丄兤亄俁/俀兾)
|丄兤亄俁/俀兾)傛偭偰倎(倝
 )亖倝(倎
)亖倝(倎 )
)
丂埲忋傛傝偄偢傟偺応崌傕倎(倝 )亖倝(倎
)亖倝(倎 )偲側傞偐傜丄曄姺倎
)偲側傞偐傜丄曄姺倎 倝偲曄姺倝
倝偲曄姺倝 倎偲偼摨偠曄姺偱偁傞偐傜倎
倎偲偼摨偠曄姺偱偁傞偐傜倎 倝亖i
倝亖i 倎偲側傞丅崱屻偼偙傟傪倎倝亖倝倎偲昞傢偡偙偲偵偡傞丅
倎偲側傞丅崱屻偼偙傟傪倎倝亖倝倎偲昞傢偡偙偲偵偡傞丅
丂師偵俀偮偺曄姺倎偲倐倝偲偺榓傪峫偊傞丅
丂丂丂倎丟 劌仺倎
劌仺倎
丂丂丂倐倝丟 劌仺倐(倝
劌仺倐(倝 )
)
傛傝
丂丂丂倎亄倐倝丟 劌仺倎
劌仺倎 亄倐(倝
亄倐(倝 )
)
偲側傞丅偙傟偼
丂丂丂倎亄倐倝丟倎 劌仺倎
劌仺倎 亄倐
亄倐 *
*
偲峫偊偰傕傛偄丅
丂偮傑傝曄姺倎亄倐倝偼 偵倎
偵倎 亄倐
亄倐 *傪懳墳偝偣傞曄姺偱偁傞丅
*傪懳墳偝偣傞曄姺偱偁傞丅
丂偙偺曄姺偺榓倎亄倐倝偼慄宆偱偁傞偙偲傪帵偦偆丅傑偢
丂丂丂倎亄倐倝丟 劌仺倎
劌仺倎 亄倐(倝
亄倐(倝 )偼倎亄倐倝丟
)偼倎亄倐倝丟 劌仺(倎亄倐倝)
劌仺(倎亄倐倝)
側偺偱偁傞偐傜
丂丂丂(倎亄倐倝) 亖倎
亖倎 亄倐(倝
亄倐(倝 )
)
偲側傞丅
丂師偵擟堄偺俀偮偺儀僋僩儖 1丄
1丄 2偵懳偟偰丄
2偵懳偟偰丄
丂丂丂倎丟 1亄
1亄 2劌仺倎(
2劌仺倎( 1亄
1亄 2)
2)
丂丂丂倐倝丟 1亄
1亄 2劌仺倐(倝(
2劌仺倐(倝( 1亄
1亄 2))
2))
偺俀偮偺曄姺傪峫偊傞丅
丂偙傟傛儕俀偮偺曄姺偺榓偼
丂丂丂倎亄倐倝丟 1亄
1亄 2劌仺倎(
2劌仺倎( 1亄
1亄 2)亄倐(倝(
2)亄倐(倝( 1亄
1亄 2))
2))
偲側傞丅
丂丂丂倎亄倐倝丟 1亄
1亄 2劌仺(倎亄倐倝)(
2劌仺(倎亄倐倝)( 1亄
1亄 2)
2)
偱偁傞偐傜丄
丂丂丂(倎亄倐倝)( 1亄
1亄 2)亖倎(
2)亖倎( 1亄
1亄 2)亄倐(倝(
2)亄倐(倝( 1亄
1亄 2))
2))
偲側傞丅
丂倝偺慄宆惈偼婛偵妋偐傔偰偁傞偺偱丄
丂丂丂倝( 1亄
1亄 2)亖倝
2)亖倝 1亄倝
1亄倝 2
2
傛偭偰
丂丂丂倐(倝( 1亄
1亄 2))亖倐(倝
2))亖倐(倝 1亄倝
1亄倝 2)亖倐(倝
2)亖倐(倝 1)亄倐(倝
1)亄倐(倝 2)
2)
廬偮偰
丂丂丂(倎亄倐倝)( 1亄
1亄 2)亖倎(
2)亖倎( 1亄
1亄 2)亄倐(倝(
2)亄倐(倝( 1亄
1亄 2))
2))
丂丂丂丂亖倎 1亄倎
1亄倎 2亄倐(倝
2亄倐(倝 1)亄倐(倝
1)亄倐(倝 2)
2)
丂丂丂丂亖倎 1亄倐(倝
1亄倐(倝 1)亄倎
1)亄倎 2亄倐(倝
2亄倐(倝 2)
2)
丂丂丂丂亖(倎亄倐倝) 1亄(倎亄倐倝)
1亄(倎亄倐倝) 2
2
偲側傝丄倎亄倐倝偺慄宆惈偑徹柧偝傟傞丅