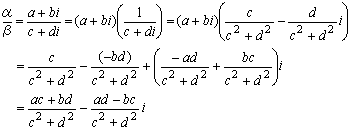(鶣)憡摍
 劌仺倎
劌仺倎 亄倐
亄倐 *
*丂們亄倓倝丟
 劌仺們
劌仺們 亄倓
亄倓 *
*偙偺俀偮偺曄姺偵偍偄偰
丂丂丂倎
 亄倐
亄倐 *亖們
*亖們 亄倓
亄倓 *
*偲偍偔偲
 偲
偲 *偺撈棫惈傛傝倎亖們丄倐亖倓偑摼傜傟傞丅偙偺偲偒俀偮偺曄姺偼摨偠曄姺偲偄偆偙偲偵側傞偺偱倎亄倐倝亖們亄倓倝傛傝倎亖們丄倐亖倓偑摼傜傟傞丅
*偺撈棫惈傛傝倎亖們丄倐亖倓偑摼傜傟傞丅偙偺偲偒俀偮偺曄姺偼摨偠曄姺偲偄偆偙偲偵側傞偺偱倎亄倐倝亖們亄倓倝傛傝倎亖們丄倐亖倓偑摼傜傟傞丅
(鶤)壛朄
丂丂丂兛丟
 劌仺兛
劌仺兛
丂丂丂兝丟
 劌仺兝
劌仺兝
傪峫偊傞丅
偙偺偲偒
丂丂丂兛亄兝丟
 劌仺兛
劌仺兛 亄兝
亄兝
偱偁傞偑丄偙傟偼
丂丂丂兛亄兝丗
 劌仺(兛亄兝)
劌仺(兛亄兝)
偱傕偁傞丅廬偭偰丄
丂丂丂(兛亄兝)
 亖兛
亖兛 亄兝
亄兝 亖(倎亄倐倝)
亖(倎亄倐倝) 亄(們亄倓倝)
亄(們亄倓倝)
丂丂丂丂亖倎
 亄倐
亄倐 *亄們
*亄們 亄倓
亄倓 *亖(倎亄們)
*亖(倎亄們) 亄(倐亄倓)
亄(倐亄倓) *
*丂丂丂丂亖(倎亄們)
 亄(倐亄倓)倝
亄(倐亄倓)倝
丂廬偮偰
丂丂丂兛亄兝丟
 劌仺(倎亄們)
劌仺(倎亄們) 廫(倐亄倓)倝
廫(倐亄倓)倝
偱偁傝丄
丂丂丂(倎亄們)亄(倐亄倓)倝丟
 劌仺(倎亄們)
劌仺(倎亄們) 亄(倐亄倓)倝
亄(倐亄倓)倝
偱偁傞偐傜曄姺兛亄兝偲丄曄姺(倎亄們)亄(倐亄倓)倝偲偼摨偠曄姺偱偁傞丅
傛偭偰
丂丂丂兛亄兝亖(倎亄倐倝)亄(們亄倓倝)亖(倎亄們)亄(倐亄倓)倝
偲側傝偙偙偵暋慺悢偺壛朄偺寁嶼婯懃偑摫偐傟傞丅
(鶥)尭朄
丂丂丂兞亖兝堦兛亖(們亄倓倝)亅(倎亄倐倝)亖(們亅倎)亄(倓堦倐)倝
偲側傞偙偲偼偡偖帵偝傟傞丅
(鶦)忔朄
 劌仺兛(兝
劌仺兛(兝 )偵偮偄偰峫偊傞丅
)偵偮偄偰峫偊傞丅丂傑偢
丂丂丂倝
 *亖(|
*亖(| |丄兤亄兾/俀)亖(|
|丄兤亄兾/俀)亖(| |丄兤亄兾/俀亄兾/俀)
|丄兤亄兾/俀亄兾/俀)丂丂丂丂亖(|
 |丄兤亄兾)亖亅
|丄兤亄兾)亖亅
偱偁傞丅
丂丂丂兛(兝
 )亖兛(們
)亖兛(們 亄倓
亄倓 *)亖(倎亄倐倝)(們
*)亖(倎亄倐倝)(們 亄倓
亄倓 *)
*)丂丂丂丂亖(倎亄倐倝)(們
 )亄(倎亄倐倝)(倓
)亄(倎亄倐倝)(倓 *)
*)丂丂丂丂亖倎(們
 )亄倐倝(們
)亄倐倝(們 )亄倎(倓
)亄倎(倓 *)亄倐倝(倓
*)亄倐倝(倓 *)
*)丂丂丂丂亖倎們
 亄倐們(倝
亄倐們(倝 )亄倎倓(倝
)亄倎倓(倝 )亄倐倓(倝
)亄倐倓(倝 *)
*)丂丂丂丂亖倎們
 亄倐們(倝
亄倐們(倝 )亄倎倓(倝
)亄倎倓(倝 )亄倐倓(亅
)亄倐倓(亅 )
)丂丂丂亖(倎們亅倐倓)
 亄(倎倓亄倐們)倝
亄(倎倓亄倐們)倝
丂丂丂(倎們亅倐倓)亄(倎倓亄倐們)倝丟
 劌仺(倎們亅倐倓)
劌仺(倎們亅倐倓) 亄(倎倓亄倐們)倝
亄(倎倓亄倐們)倝
偱偁傞偐傜曄姺兛兝偲曄姺(倎們亅倐倓)亄(倎倓亄倐們)倝偲偼摨偠曄姺偱偁傞丅
傛偭偰
丂丂丂兛兝亖(倎亄倐倝)(們廫倓倝)亖(倎們亅倐倓)亄(倎倓亄倐們)倝
偲側傞丅
偙偺幃偐傜暋慺悢偺忔朄偑壜姺偱偁傞偙偲傕傢偐傞丅
(鶧)彍朄
丂丂丂倂亖侾/(倎亄倐倝)
偲掕媊偡傞丅倂亖倫亄倯倝偲偍偄偰婛偵妋偐傔傜傟偨彅懱幙傪傕偲偵偟偰寁嶼偟偰傒傛偆丅
(倎亄倐倝)倂亖(倎亄倐倝)(倫亄倯倝)亖侾偲偍偔偲
丂丂丂(倎倫亅倐倯)亄(倎倯亄倐倫)倝亖倢
偲側傞丅傛偭偰
丂丂丂倎倫亅倐倯亖侾丄倎倯亄倐倫亖侽
偑摼傜傟
丂丂丂倫亖倎/(倎2亄倐2)丄倯亖亅倐/(倎2亄倐2)
偲側傞丅傛偭偰
丂丂丂倂亖倫亄倯倝亖倎/(倎2亄倐2)亅倐倝/(倎2亄倐2)
偲側傞丅偮傑傝
丂丂丂倎亄倐倝亖倎/(倎2亄倐2)亅倐倝/(倎2亄倐2)
偲側傞丅偦偙偱暋慺悢偺彍朄傪師偺傛偆偵掕媊偡傞丅
丂丂丂