丂弖娫懍搙傪媮傔傞
丂
丂慜夞媮傔偨暯嬒懍搙偼丄傕偪傠傫偁傞帪娫偺偁偄偩偺暯嬒偺懍搙偱偁偭偰丄偪傚偆偳侾昩屻丄俀昩屻丄俁昩屻丒丒丒偺弖娫偺懍搙偱偼側偄丅
丂偦偙偱椺偊偽偪傚偆偳俁昩屻偺懍搙傪峫偊傞偨傔偵丄傑偢傕偭偲傕偭偲帪娫偺暆傪彫偝偔偟偨暯嬒懍搙傪媮傔偰傒傞丅
栤戣丂倶昩屻傑偱偺棊壓嫍棧倷偑丂倷亖倶俀偱偁傜傢偝傟傞幬柺傪偙傠偑傞塣摦偵偮偄偰丄俁昩屻偐傜偺帪娫偺暆傪彫偝偔偟偨師偺暯嬒懍搙傪媮傔側偝偄丅
| 帪娫丂丂倶昩 | 丂丂俁丂丂丂丂3.001丂丂丂丂3.01丂丂丂丂3.1丂丂丂丂 |
|---|---|
| 埵抲丂丂倷cm | 丂丂俋丂丂丂乮丂丂丂乯丂丂丂乮丂丂丂乯 丂丂9.61丂丂丂丂丂丂 |
丂俁昩屻偐傜俁丏侾昩屻傑偱偺暯嬒懍搙丂丂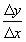 亖
亖
丂俁昩屻偐傜俁丏侽侾昩屻傑偱偺暯嬒懍搙丂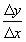 亖
亖
丂俁昩屻偐傜俁丏侽侽侾昩傑偱偺暯嬒懍搙丂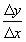 亖
亖
幙栤丂帪娫偺憹暘倛傪偳傫偳傫彫偝偔偟偰偄偗偽暯嬒懍搙偼偁傞抣偵偳傫偳傫嬤偯偄偰偄偔丅偙偺傛偆偵偟偰偄偮偐偼弖娫懍搙偑媮傔傜傟傞偩傠偆偐丅
丂丂丂偁丂媮傔傜傟傞
丂丂丂偄丂媮傔傜傟側偄
丂丂丂偆丂弖娫偵偼塣摦偟偰偄側偄偺偱懍搙偲偄偆傕偺偼側偄
丂俁昩屻偐傜俁丏侾昩屻偺暯嬒懍搙丒丒丒丒丒俇丏侾倣乛昩
丂俁昩屻偐傜俁丏侽侾昩屻偺暯嬒懍搙丒丒丒丒俇丏侽侾倣乛昩
丂俁昩屻偐傜俁丏侽侽侾昩屻偺暯嬒懍搙丒丒丒俇丏侽侽侾倣乛昩
丂丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
偲丄俁昩屻偐傜偺帪娫偺暆傪偳傫偳傫彫偝偔偟偰偄偗偽丄暯嬒懍搙偼偳傫偳傫俇倣乛昩偵嬤偯偄偰偄偔丅偦偙偱帪娫偺憹暘傪倛偲偟偰丄俁昩屻偐傜俁亄倛昩屻傑偱偺暯嬒偺懍搙傪媮傔丄倛偺抣傪尷傝側偔侽偵嬤偯偗傞偙偲傪峫偊傞丅
栤戣丂倷亖倶俀偱偁傜傢偝傟傞幬柺偺棊壓塣摦偵偮偄偰丄俁昩屻偐傜俁亄倛昩屻傑偱偺暯嬒懍搙傪媮傔側偝偄丅
| 帪娫丂丂倶昩 | 丂丂俁丂丂丂丂俁亄倛丂丂丂丂 |
|---|---|
| 埵抲丂丂倷cm | 丂丂俋丂丂丂丂丂丂 |
丂偙偺偲偒倛偑尷傝側偔侽偵嬤偯偔偲偒暯嬒懍搙偼尷傝側偔 俇倣乛昩偵嬤偯偔丅偙偺抣丂俇倣乛昩傪丄俁昩屻偺弖娫懍搙偲峫偊傞丅
丂偝傜偵偙偺傛偆側抣傪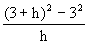 偺嬌尷抣偲偄偄丄婰崋倢倝倣傪梡偄偰師偺傛偆偵昞傢偡丅
偺嬌尷抣偲偄偄丄婰崋倢倝倣傪梡偄偰師偺傛偆偵昞傢偡丅
丂丂丂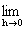
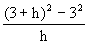 亖俇
亖俇
楙廗丂師偺嬌尷抣傪媮傔傛丅
丂嘆丂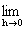 乮倛俀亅俇倛亄俈乯亖
乮倛俀亅俇倛亄俈乯亖
丂嘇丂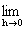 乮倛俀亅俁乯亖
乮倛俀亅俁乯亖
丂嘊丂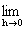 乮倛俀亄俆倛亅侾乯亖
乮倛俀亄俆倛亅侾乯亖