旝暘學悢偲摫娭悢
丂堦斒偵丄娭悢倖乮倶乯偱倶偑倎偐傜倎亄倛傑偱曄傢傞偲偒偺暯嬒曄壔棪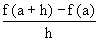 偵偍偄偰丄倛仺侽偺偲偒偺嬌尷抣 倢倝倣 傪娭悢倖乮倶乯偺倶亖倎偵偍偗傞旝暘學悢傑偨偼曄壔棪偲偄偄丄婰崋倖乫乮倎乯偱昞傢偡丅
偵偍偄偰丄倛仺侽偺偲偒偺嬌尷抣 倢倝倣 傪娭悢倖乮倶乯偺倶亖倎偵偍偗傞旝暘學悢傑偨偼曄壔棪偲偄偄丄婰崋倖乫乮倎乯偱昞傢偡丅
|
掕媊丂堦斒偵丂偁傞娭悢倷亖倖乮倶乯偺倶亖倎偵偍偗傞旝暘學悢 丂丂丂倖乫乮倎乯亖 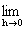 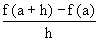
|
楙廗栤戣
| 丂帪娫丂丂丂倶昩丂 | 丂丂丂侾丂丂丂丂丂侾亄倓倶丂丂丂 |
|---|---|
| 丂嫍棧丂丂丂倷倣丂 | 丂丂丂侾丂丂丂丂丂丂丂丂丂丂丂丂 |
丂丂丂 丂 丂
| 丂帪娫丂丂丂倶昩丂 | 丂丂丂俀丂丂丂丂丂俀亄倓倶丂丂丂 |
|---|---|
| 丂嫍棧丂丂丂倷倣丂 | 丂丂丂俀丂丂丂丂丂丂丂丂丂丂丂丂 |
| 丂帪娫丂丂丂倶昩丂 | 丂丂丂係丂丂丂丂丂係亄倓倶丂丂丂 |
|---|---|
| 丂嫍棧丂丂丂倷倣丂 | 丂丂丂係丂丂丂丂丂丂丂丂丂丂丂丂 |
丂偙偺傛偆偵倷亖倶俀偺幬柺偺棊壓塣摦偵偍偄偰丄
丂丂丂丂侽昩屻偺弖娫懍搙丂侽倣乛昩
丂丂丂丂侾昩屻偺弖娫懍搙丂俀倣乛昩
丂丂丂丂俀昩屻偺弖娫懍搙丂係倣乛昩
丂丂丂丂俁昩屻偺弖娫懍搙丂俇倣乛昩
丂丂丂丂係昩屻偺弖娫懍搙丂俉倣乛昩
丂丂丂丂丂丂丂丒丒丒丒丒丒
偲側偭偰丄帪娫偵懍搙偑斾椺偟偰偄傞傛偆偵巚偊傞丅偙偺偙偲傪妋偐傔傞偨傔偵丄堦斒偵倶昩屻偺弖娫懍搙傪昞傢偡幃傪媮傔偰傒傛偆丅
栤戣丂倷亖倶俀偱昞傢偝傟傞幬柺偺棊壓塣摦偵偮偄偰丄倶昩屻偺弖娫懍搙傪媮傔傛丅
| 丂帪娫丂丂丂倶昩丂 | 丂丂丂倶丂丂丂丂丂倶亄倓倶丂丂丂丂 |
|---|---|
| 丂嫍棧丂丂丂倷倣丂 | 丂丂丂倶俀丂丂丂丂丂丂丂丂丂丂丂丂 |
丂倶昩屻偺嫍棧倷倣傪昞傢偡倷亖倖乮倶乯偵懳偟丄倶昩屻偺懍搙傪昞傢偡娭悢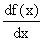 傪娭悢倖乮倶乯偺摫娭悢偲偄偆丅
傪娭悢倖乮倶乯偺摫娭悢偲偄偆丅
丂丂偙傟傪倖亴乮倶乯偲偐倷亴偲傕昞傢偡丅
 栤戣丂倷亖倶俀偱昞傢偝傟傞幬柺偺棊壓塣摦偵偮偄偰丄倶昩屻偺弖娫懍搙傪昞傢偡摫娭悢倷亴亖俀倶丂偺僌儔僼傪彂偗
栤戣丂倷亖倶俀偱昞傢偝傟傞幬柺偺棊壓塣摦偵偮偄偰丄倶昩屻偺弖娫懍搙傪昞傢偡摫娭悢倷亴亖俀倶丂偺僌儔僼傪彂偗
丂嘇丂俆昩屻丄俇昩屻偺弖娫懍搙傪媮傔側偝偄
栤戣丂抧媴忋偺帺慠棊壓塣摦偱偼丄倶昩屻偺嫍棧倷倣偼偍傛偦丂倷亖俆倶俀偱昞傢偝傟傞丅偙偺偲偒偺倶昩屻偺弖娫懍搙倷亴倣乛昩 傪昞傢偡摫娭悢傪媮傔傛丅
| 丂帪娫丂丂丂倶昩丂 | 丂丂丂倶丂丂丂丂丂倶亄倓倶丂丂丂 |
|---|---|
| 丂嫍棧丂丂丂倷倣丂 | 丂丂俆亊俀丂丂丂丂丂丂丂丂丂丂丂 |
丂嘇侾昩屻俀昩屻俁昩屻偺弖娫懍搙傪媮傔側偝偄丅
栤戣丂堦斒揑偵丂倷亖倎倶俀 偺摫娭悢倷亴傪媮傔側偝偄丅
| 丂帪娫丂丂丂倶昩丂 | 丂丂丂倶丂丂丂丂丂倶亄倓倶丂丂丂 |
|---|---|
| 丂嫍棧丂丂丂倷倣丂 | 丂丂倎倶俀丂丂丂丂丂丂丂丂丂丂丂 |
|
岞幃侾丂娭悢丂倷亖倎倶俀丂偺摫娭悢偼 丂丂丂丂丂丂丂丂丂倷亴亖 |
楙廗栤戣丂師偺娭悢偺摫娭悢傪媮傔傛丅
丂嘆丂倷亖俁倶俀
丂嘇丂倷亖係倶俀
丂嘊丂倷亖俈倶俀
丂嘋丂倷亖4.9倶俀
丂丂丂 丂 丂