外サイクロイド曲線

　それでは今みた様々なサイクロイド曲線のうちで、外サイクロイド曲線（Epicycloid）を取り上げ、パラメータの変化と曲線の関係について考えてみましょう。

　定円の半径をａ、その円周上を転がる動円の半径をｂとします。このとき、この曲線の方程式を媒介変数であらわすと次のようになります。これは下の図より導き出すことができます。

　

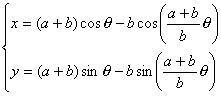
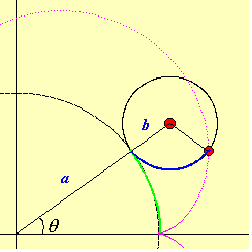
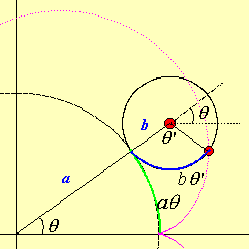
　さて、2つのパラメータを変化させて描き出す曲線の様子を調べてみましょう。

　 　

　 　

　 　

　 　

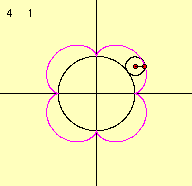
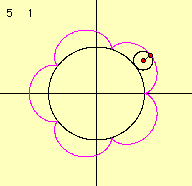
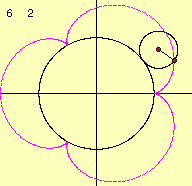
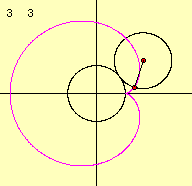
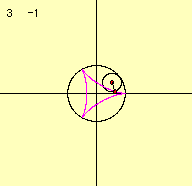
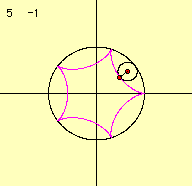
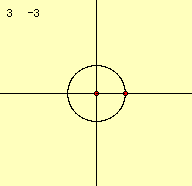
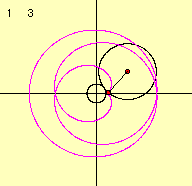
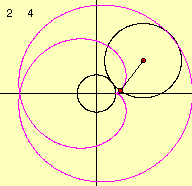
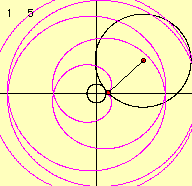
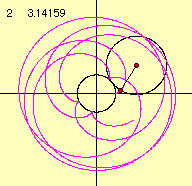
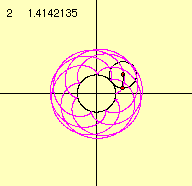
　これらのデータより、描き出される図形の形は係数ａとｂの比によって変化していくことがわかります。　ｍ＝ａ／ｂとすると、

1. ｍが正の整数のとき　　定点の周りの外回りのｍ個の枝からなる
2. ｍが負の整数のとき　　定点の周りの内回りのｍ個の枝からなる
3. ｍが分数のとき　　　　動点は有限個の枝を描いて最初の状態に戻る
4. ｍが無理数のとき　　　複雑な動きになり、枝の数が無数になる