4�D�i�r�Q�[�^�Ƃ��Ắu���w�ʎ蔠�v
4_1�D�����ЂƂ̃R���Z�v�g
�@�uM.Sanae'S HomePage�v�ɂ͐��w�ƃ\�t�g�E�G�A�ɂ��Č����Ă������Ƃ����R���Z�v�g�ȊO�ɁC�����ЂƂ̑��ʂ�����D���ꂪ�u���w�ʎ蔠�v�ł���D�܂��͑O�����Љ�悤�D
�@"���w"�ƕ����������Ŋ�������߂�l�������Ǝv���܂��B�������C�����C�ؖ��c���̍s�������Ƃ���͎H�@���w�ɂ��p�Y���␄�������̂悤�Ɋy����������C�킭�킭����悤�Ȃ���ȂƂ��������̂ł͂Ȃ��ł��傤���B�����C�w�Z�̎��Ƃł͂���Ȋy���݂��`���ɂ����_������̂������ł��B
�@���w�̒��ɐ��ޑ����̃g�s�b�N���W�߂Ă�������C�Ǝv�����̃y�[�W�����܂��B���̐��قǂ���b����W�߂�̂͑�ςł��B�ł�����C���̃y�[�W�͏ł炸�C��������ƍ���Ă������ƍl���Ă��܂��B�N�ł��m���Ă��邻��Șb�肩�班�����E�E�E�B
�@�܂��C�l�b�g���[�N�^���ރf�[�^�x�[�X�u���w�̂����݁v�̒��Ɏ��߂��Ă���l�X�Șb����C�_�C�W�F�X�g�ɂ��Ȃ���Љ�Ă��������Ǝv���܂��B���Ƃ��Ƃ̘b��̃A�h���X���ڂ��Ă����܂��̂ŁC�����������킯�Ζ{�҂̃y�[�W�ŏڂ������ׂĂ݂Ă��������B
�@�u���w�̂����݁v�̃~�j�`���A�ŁC����𐔊w�\�t�g����g���邱�ƂŁC���Viasual�ɍČ����Ă����D���ꂪ�uM.Sanae'S HomePage�v�̂�����̃R���Z�v�g�Ƃ�����D
4_2�D���r�W���A���ɁC���R���p�N�g��
 �@���̃y�[�W�͐��w�̒��ɐ��ޗl�X�Șb������r�W���A���ɏЉ�C���w�ɑ��鋻���E�S�������o���Ă������Ƃ����ړI������D���k�ւ̃A�N�Z�X�ɂ��Ă͗��K����P���e�X�g�̗��Ɉ�����C���w�ʐM�I�ȐF�����̕��ƂȂ��Ă���D���Ƃ̒��Ńg�s�b�N�I�Ɏ��グ�C���Ƃ̓��e�ƃv�����g�Ƃ��^�C�A�b�v�����Đ��k�ɏЉ�Ă���D�Ⴆ�Ί��̒P���Łu�u���b�N�{�b�N�X�v��p���Ċ�f(x)���������Ƃ��ɁC"����"�Ƃ��Ă̋�������ۂɏЉ�Ȃ���C���̂܂Ƃ߂Ƃ��ăv�����g�Ő�������Ȃǂ���ƌ��ʂ��傫�������Ǝv����D
�@���̃y�[�W�͐��w�̒��ɐ��ޗl�X�Șb������r�W���A���ɏЉ�C���w�ɑ��鋻���E�S�������o���Ă������Ƃ����ړI������D���k�ւ̃A�N�Z�X�ɂ��Ă͗��K����P���e�X�g�̗��Ɉ�����C���w�ʐM�I�ȐF�����̕��ƂȂ��Ă���D���Ƃ̒��Ńg�s�b�N�I�Ɏ��グ�C���Ƃ̓��e�ƃv�����g�Ƃ��^�C�A�b�v�����Đ��k�ɏЉ�Ă���D�Ⴆ�Ί��̒P���Łu�u���b�N�{�b�N�X�v��p���Ċ�f(x)���������Ƃ��ɁC"����"�Ƃ��Ă̋�������ۂɏЉ�Ȃ���C���̂܂Ƃ߂Ƃ��ăv�����g�Ő�������Ȃǂ���ƌ��ʂ��傫�������Ǝv����D
�@���グ�Ă�����e�͎����g������܂ł̂��Ȃ��o���̒�����|���Ă������̈ȊO�ɁC�����́u���w�̂����݁v�̒��ŏЉ��Ă������̂��_�C�W�F�X�g�ɂ��ďЉ�Ă���D�O�q�����悤�Ɂu���w�̂����݁v�͒n���ɐςݏd�˂Ă������̒~�ς��c��ȗʂƂȂ�C�ꌩ���������ł͂��̑S�̑���c�����邱�Ƃ�����ɂȂ��Ă��Ă��܂��Ă���D�܂�������̃��|�[�g�𒆐S�Ƃ��Čf�ڂ��Ă��邽�߁C���e����ʌ����Ƃ��čl�����ꍇ������̂������D���̂��߂����ƃR���p�N�g�ɁC��蕪����₷����ʌ����ɂ���K�v�����܂ꂽ�D���ꂪ�u���w�ʎ蔠�v�Ȃ̂ł���D
4_3�D�ǂ�ȓ��e��
�u���w�ʎ蔠�v�Ɏ��߂��Ă�����e�͂ǂ����ʓI�Ȃ��̂���ł���D��ʓI�ł͂��邪�ł��邾��Visual�ɂȂ�悤�ɐS�����Ă���D��ނ͌��݂̏�100�ȏオ���߂��Ă��邪�C�����炸��������ƈ�ĂĂ������ƍl���Ă���D���Ɏ��^����Ă�����e���炢�����Љ�����D�iAPPENDIX_2�@�u���w�ʎ蔠 CONTENTS�v�Q���j
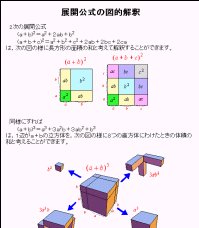
- �W�J�����̐}�I����
(a�{b)3�̓W�J�������C1�ӂ�a�{b�̗����̂�8�̒����̂ɂ킯���Ƃ��̑̐ς̘a�ƍl��Visual�ɐ�������D
- 2��3�����̓W�J
(a+b)n�̓W�J���Ɍ����p�X�J���̎O�p�`�D�����(a+b+c)n�܂Ŋg�����C���̓I�ȃp�X�J���̎O�p�`�����������D
- 2���������̉�����}����
�^����ꂽ�����������������Ɏ���2���������D���̉���}������ɂ͂ǂ�������悢���D
- �u���b�N�{�b�N�X
�_���{�[���ō���������̔������C��������牽��������ƁC���̒��ł��铭�������ďo������o�Ă���D����ȃu���b�N�{�b�N�X�����ۂ̎ʐ^�Ő����D
- �O�p�`�̏d�S�ƃA�t�@�C���ϊ�
�d�S�͊e������2�F1�̔�ɓ������鐫�����C�ϊ��̐��������Ƃɑ��ȂŐ�������D
- �J���̕`���O���t�B�b�N�X
��C�̃J����p���ĕ��ʏ�ɐ}�`��`�悷��\�t�g�u���S�v�D�ł��厖�ȃ|�C���g��"�J���̗���ɗ�����"�l���Ă����邱�ƁD
- ���ȁI�e�g���p�b�N
�������̍u�K��ŋ����Ă������������ȁC���l�ʑ̂̍����D�i���ۂɂ̓e�g���p�b�N�����l�ʑ̂ł��邱�Ƃɒ��ӁI�j
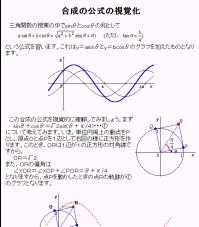
- 3�{�p�̌���
3�{�p�̌����͊o���Â炭�C���܂�ʔ��݂̂Ȃ������Ƃ�����D���̌�����2�̊ϓ_����l���Ă����D
- 3�����O���t�B�b�N�X�Ō���x���}
�W���̈�ʓI�ȊW��\�킷�̂ɗp����"�x���}"�D���i�͊ۂ��~��p����Ƃ����3DCG�őN�₩�ɕ`���Ă݂�D
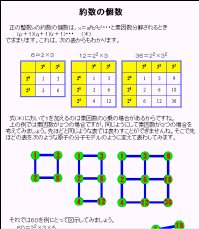
- �̌�
���̐���x��apbqcr����̖̌���(p+1)(q+1)(r+1)�ŋ��܂邪�C�����3�������q���f�����g���Đ�������D
- ��k2�̐}�I����
��k2�̌�����}�I�ɊȒP�ɉ��߂�����@��2�Љ�D
- 00���C���[�W������
�w���̊w�K��a��0�̂Ƃ�a0��1�ƏK�����C�ł�00�͂�����ɂȂ�̂ł��낤���D3�����}�`�����Ƃ�Visual�ɐ�������D
- �ςݖ��d�˂�
y=ex �̃O���t��y=xn�̐ςݖO���t��ςݏd�˂ċߎ����Ă݂�D
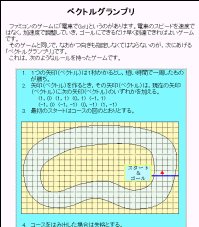
- �x�N�g���O�����v��
�����Ƒ傫�����w�肵�Ė����w�肵�āC�R�[�X���ł��邾�����Ȃ��{���Ŏ�������D
- �ꎟ�Ɨ����g�����
�x�N�g���̈ꎟ�Ɨ������g���������C���w�Z�̗��Ȃ̎��ƂŏK�����Ă��̌�����p���ĉ����Ă����D
- ���~�̃C���[�W��
�ux2+y2=�|1�ĉ~�͂ǂ�ȉ~�H�v�@���E�������ʂ��狕���ʂւƍL���邱�ƂŁC�V���ȁu���~�v�̐��E���_�Ԍ���D
- �g�ʂɂ݂�2���Ȑ�
�r�ɏ��𓊂����ꂽ�Ƃ��ɂł���g�ʁD���̒��ɉB��Ă���2���Ȑ����l����D
- ���낢��ȕϊ�
1���ϊ��ɂ���ĕ\�킷�s���ς��邱�Ƃɂ���āC�ŏ��̊G���ǂ̂悤�ɕω����Ă������H


�@
4_4�D�i�r�Q�[�^�Ƃ��Ă̖���
�@�C���^�[�l�b�g�͈�Ċw�K�Ƃ��Ă̊w�K��i�Ƃ��Ă͂��Ȃ�s�����ł���ƍl������D�������C�l�̊w�K�Ƃ��Ă͍l�����Ȃ��قǂ̈З͂�����̂ł͂Ȃ��낤���D�l�b�g��ʂ��Ď����ɂƂ��ėL�p�ȏ����W�߂�C�ŐV�̏�z�M�����C�킩��Ȃ����������[���œ������������̈ӌ�������D�C���^�[�l�b�g�͗l�X�ȉ\�����߂Ă���D���̒��ł������W�߂�Ƃ������ʂ́C����܂ł�"����"�Ƃ����}�̂�ʂ��čs���Ă�����Ƃ����Ȃ�ϗe�������Ƃ�����D�l�b�g�ł͂��̏�����C�L�͈͂ɓ��������ł͂Ȃ��C�e�L�X�g�x�[�X�ł����������摜�≹�����͂��߂Ƃ����}���`���f�B�A�ւƁC�����Java�CVRML�Ȃǂ̃\�t�g�E�G�A��p���Ă��C���^���N�e�B�u�ɓ����邱�ƂƂȂ����D
�@�����Ŗ��ɂȂ�̂͂��������L�p�ȏ���@���ɂ��Ď�ɓ���邩�C�Ƃ������Ƃł���D���R�����V�X�e�����g���Ă��ł��邪�C�����ɂƂ��ėL�p���Ǝv����������ɓ���邾���ł��ĊO���Ԃ���������̂ł���D��������"���݂̍肩"�k�Ƀi�r�Q�[�g���邱�Ƃ��C���t�Ƃ��Ă̑厖�Ȏd���ɂȂ��Ă����̂ł͂Ȃ��낤���D�u���w�ʎ蔠�v�Ɏ��߂��Ă����ނ́C�ł��������p���Ă���"�݂肩"������悤�ɂ��Ă���D����"�݂肩"�͈ȑO�̂悤�ȏ����ł͂Ȃ��C�l�b�g��ɂ�����"�A�h���X"�Ȃ̂ł���D��������������Ă������Ƃ����ꂩ��͋��߂���̂ł͂Ȃ��낤���D
 �@���̃y�[�W�͐��w�̒��ɐ��ޗl�X�Șb������r�W���A���ɏЉ�C���w�ɑ��鋻���E�S�������o���Ă������Ƃ����ړI������D���k�ւ̃A�N�Z�X�ɂ��Ă͗��K����P���e�X�g�̗��Ɉ�����C���w�ʐM�I�ȐF�����̕��ƂȂ��Ă���D���Ƃ̒��Ńg�s�b�N�I�Ɏ��グ�C���Ƃ̓��e�ƃv�����g�Ƃ��^�C�A�b�v�����Đ��k�ɏЉ�Ă���D�Ⴆ�Ί��̒P���Łu�u���b�N�{�b�N�X�v��p���Ċ�f(x)���������Ƃ��ɁC"����"�Ƃ��Ă̋�������ۂɏЉ�Ȃ���C���̂܂Ƃ߂Ƃ��ăv�����g�Ő�������Ȃǂ���ƌ��ʂ��傫�������Ǝv����D
�@���̃y�[�W�͐��w�̒��ɐ��ޗl�X�Șb������r�W���A���ɏЉ�C���w�ɑ��鋻���E�S�������o���Ă������Ƃ����ړI������D���k�ւ̃A�N�Z�X�ɂ��Ă͗��K����P���e�X�g�̗��Ɉ�����C���w�ʐM�I�ȐF�����̕��ƂȂ��Ă���D���Ƃ̒��Ńg�s�b�N�I�Ɏ��グ�C���Ƃ̓��e�ƃv�����g�Ƃ��^�C�A�b�v�����Đ��k�ɏЉ�Ă���D�Ⴆ�Ί��̒P���Łu�u���b�N�{�b�N�X�v��p���Ċ�f(x)���������Ƃ��ɁC"����"�Ƃ��Ă̋�������ۂɏЉ�Ȃ���C���̂܂Ƃ߂Ƃ��ăv�����g�Ő�������Ȃǂ���ƌ��ʂ��傫�������Ǝv����D




