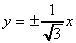直線 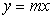 と円 と円 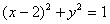 が異なる2点で交わっている。 が異なる2点で交わっている。(1) mの値の範囲を定めよ。 (2) mの値が変化するとき、線分ABの中点Pはどのような図形上を描くか。その図形の方程式を求めよ。 |
(解)(1) 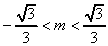
(2)
(解説)この問題もパラメータmの変化に伴う軌跡の問題である。実際に点Pの座標をパラメータmで表示しても、その後が難しい。解法の1つの方法として、パラメータmの値の変化から表される図形の結果を予測して、その結果からそれにあった解法を探し出すというやり方もある。
この問題も円になることが予測されるが、その円の中心と半径はどうなるのであろうか。A,Bの中点Pについて、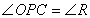
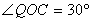
ゆえに、接線の方程式は