��TOP�@BACK�@NEXT��
2�@���w�p�t���[�E�G�A��p�������w���ލ쐬�̋�̗�
�@�����_�Ŏ��ƂɎg�p�ł���t���[�E�F�A�̃c�[���̒����牺�L�̂R�{�����̋��ލ쐬��Ƌ��ɏЉ�܂��D������̃c�[�������̊J���҂̔M�ӂ���������f���炵���\�t�g�ł��D
�@�܂������̃c�[�������ʓI�Ɏg���ɂ́C���ތ����ɂ�������Ɨv�_�m�����C���ꂼ��̃\�t�g�̓�����c�����������Ŏg�������Ă������Ƃ��d�v�ł��D
�����g�p�\�t�g�ꗗ����
| �\�t�g�� |
Function View |
Grapes |
Geometric Constructor/Win
Geometric Constructor/Java |
| Version |
ver.4.43d |
ver.6.00 |
ver. 1.7.2 |
| ���쌠�� |
�a�c�@�[��
(�Q�n���ː��H�ƍ����w�Z) |
�F�c�@���v
(��㋳���w���������w�Z�r�c�Z��) |
�ѓ��@�N�V
(���m�����w���w����) |
�g�pOS
���J������ |
Windows95, 98, Me WindowsNT, 2000, XP
��Borland Delphi |
Windows95, 98, Me WindowsNT, 2000, XP
��Borland Delphi |
Windows95, 98, Me WindowsNT, 2000, XP
��GC/Win�`Visual Basic
GC/Java�`Java |
ΰ��߰��
URL |
http://hp.vector.co.jp/authors
VA017172/index.htm |
http://www.osaka-kyoiku.ac.jp/
~tomodak/grapes/index.html |
http://www.auemath.aichi-edu.ac.jp/
teacher/iijima/gc/
test-gcwin/download.htm |
| �p�r |
���O���t�\�� |
���O���t�\�� |
�}�`��}�c�[�� |
| �Ĕz�z�̏��� |
�Ĕz�z���R |
�Ĕz�z���R�@(�����t��) |
�����ړI�ȊO�̔z�z�֎~ |
2_1�@��}�c�[���uGeometricConstructor�v
2_1_1�y���@���z
�@GC�͒P�Ȃ�u�����^(�Эڰ���)�^�v�\�t�g�ł͂���܂���D�ܘ_���̂悤�ɂ��g���܂����C�u�����w�K�^�v�u�������^�v�Ȃǂ̑���ɂ킽��w�K�`�ԂŎ��Ƃ�W�J����ۂɂ��L���ł��D�ܘ_�C���̍ۂɋ��ނ̕��́C����̎d���Ȃǂ��g�[�^���ɍl���Ă����K�v�����邱�Ƃ͌����܂ł�����܂���D����܂Œ��w�Z�ň����Ă����}�`�Ɋւ��鋳�ނ�����15�N�x����̐V�J���ō��Z�ֈڍs���Ă��܂����C���̐}�`����������c�[���Ƃ��Ăf�b�͎��т������Ă��Ă��܂��D�ȉ�GC�}�j���A���������̔����ł��B
 �u���Ɓv�ł̗��p�̂��߂̃\�t�g
�u���Ɓv�ł̗��p�̂��߂̃\�t�g
�搶������,���k������,�v���W�F�N�^����Ĉ�̐}�ɂ��ċc�_������,�O���[�v�Œ��ׂ��肷����ł��B�K�v�ɉ�����,�搶���w����������,���[�N�V�[�g��z�����肷����ł��B�����ĉ�����,���k�̎v�l��W���Ȃ����Ƃ��d�v�ł��B�����������w�I�T���������������Ƃ��������g�̎v���⌻��̐搶������Ǝ��H�f�����Ȃ���,�u���Ɓv�ł̎g���₷����Nj����Ă������Ƃ���\�t�g�ł��B
- �C���^�[�l�b�g�Ƃ̘A�g
GC�̓\�t�g��P�ƂŎg���Ƃ�������,�C���^�[�l�b�g��ɂ��낢��Ȏ�������,������g���Ă��炤���Ƃ�z�肵�Ă���\�t�g�ł��B��}�c�[�����g�������ޓW�J�C���Ɨ�Ȃǂ͉��L��HP���Q�l�ɂ��Ă��������D
�@���uGC Forum�v�@http://www.auemath.aichi-edu.ac.jp/teacher/iijima/index.htm
- ���܂��܂Ȋ��ŗ��p�ł���\�t�g
���݁CGC�ɂ�,����3��ނ�����܂��BGC/DOS, GC/Win, GC/Java�B
�����̂ǂꂩ���g���C�����炭�قƂ�ǂ̊w�Z�Ŏg�����Ƃ��ł���Ǝv���܂��B�������,�f�[�^��(�ꕔ�@�\������)���ʂł���,�l�X�Ȍ`�ŘA�g������悤�ɂ��Ă��܂��B
- �L�[�{�[�h������\�ȃ\�t�g
- ��{�́u�ό`�v���u�P�_�̕ό`�v�ł����C�u�����̓_�����v���Ƃ��\
- �L�x�ȍ�}�@�\��
�@�E��͊I�Ȑ}�`�w����\�����C�@�}�`�̊I��������̎w�肪�L�x�D
�@�E���k�̎v�l���d�����C�����w�K�I�Ȋ����
- �����C�p�x�C�ʐρC�����ȂǍ�}�����}�`�Ɋւ��鑪��@�\��
- ��}�����}�`�́C�}�E�X�E�L�[�{�[�h�ŊȒP�ɓ������O�Ղ��ݒ�\
 �@
�@
2_1_2�@�y���ލ쐬��z
| �s��P�t����2�������̕`���O�Ձ`����ɂ��Q���Ȑ��̕`�� |
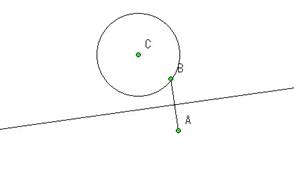
�i����P�j�uFig.1�œ_A�����E�ɓ������Ɖ��������Ă��܂����H�v
 |
 |
| (Fig.1) |
�i����Q�j�u�_A���~��������Ƃ��C���������Ă��܂����D�@����ɉ~�̈ʒu��ς���Ƃǂ��Ȃ�ł��傤�v
 |
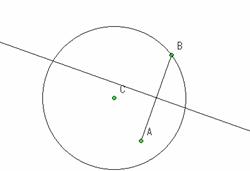 |
| �iFig.2�j |
�iFig.3�j |
���쐬�菇�T�v��
- �Q�_A�CB���Ƃ�@��[��}]��[�_]��[�V�����_�̒lj��@([Ctrl]+F����)]
- �Q�_A�CB�����Ԑ����������@��[��}]��[��������p�`]�@��[2�_������]
��[Fig.1]�_A����ō��E�ɓ�����
- ����������ɂ́C�_A��ʼnE�{�^�����N���b�N���u�_A�̃L�[�{�[�h�ό`�v���g���ƕ֗�
- [�O��]��[�ݒ�]��[����]�i[Shift]+[F2]���j���琂��������I������'�O�Ղ̐F'��'��'�ɐݒ肷��D���ۂɋO�Ղ�\������ɂ�[F9]�������ĕ\���@�\��On�ɂ���D�\�����Ă���O�Ղ���������ɂ́D[Shift]+[F9]�������D
��[Fig.2]�C[Fig.3]�_A���~����œ�����
- �_A���~����ɐݒ肷��@��[�ҏW]��[�_(��������)](�_A��I��)��[�~��ɂƂ�](�~��I��)
�����̑�������Ȃ��Ƃ�[Shift]�L�[�������Ȃ���}�E�X�œ_���ړ�������ƁC�ߐڂ����~(����)����ړ��\
| �s��Q�tw=1/z�ɂ��ϊ��ŕ��f��z�͂ǂ̂悤�ɕϊ�����邩 |
�@�����1_6�ō�p�f�Ƃ��Ă̐}�`�ϊ����\�iBasic�ōs�������ނł��D���̕ϊ��́u�P�ʉ~�Ɋւ��鋤�]�ϊ��v�ɂȂ��Ă��蕽�s�ړ��C��]�ȂǂƂ͈قȂ萶�k�ɂƂ��ăC���[�W���ɂ������ނł��D���̕ϊ��ɂ��Ă̗��_�I���ʂ͎��̃��|�[�g���Q�l�ɂȂ�܂��D�ł͂��̋��ނ̃C���[�W�����f�b�ōs���Ă݂܂��傤�D
�@�@���u���r�E�X�̂킾���v�i���������j�@http://www.nikonet.or.jp/spring/mebius/mebius.htm
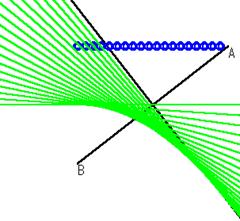
 �i����P�j�u�_z����������Ƃ��̑�1/z�̋O�Ղ́v
�i����P�j�u�_z����������Ƃ��̑�1/z�̋O�Ղ́v
�@(�)���������_��ʂ�Ȃ��Ƃ�
�@(�)���������_��ʂ�Ƃ�
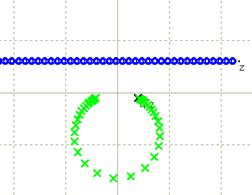
�i����Q�j�u�_z���C�~������Ƃ��̑�1/z�̋O�Ղ́v
�@(�)���_���~�̊O���ɂ���ꍇ
�@(�)���_���~�̓����ɂ���ꍇ
�@(�)���_��ʂ�ꍇ
�@��������Ă���̍l����Ԃ��ɂ��������̂ł��D���̒i�K�ł�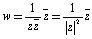 �̂悤�Ȑ����ł͂Ȃ��C���ۂɐ��k���g���_�������ƂŃC���[�W�����܂������Ƃ���ł��D�iFig.4�j
�̂悤�Ȑ����ł͂Ȃ��C���ۂɐ��k���g���_�������ƂŃC���[�W�����܂������Ƃ���ł��D�iFig.4�j
�@�����͂��̌�ŗ��_�⋭�������ʂœo�ꂷ���ł��D
���쐬�菇�T�v��
- ���W�{���f���p�ɐݒ�@��[�ް�]��[���f���p]
- �V�����_���Ƃ薼�O��z�Ƃ���
��[�ҏW]��[�_](�_A��I��)��('���O'��'z'��)
- �_1/z���Ƃ�C���O��'1/z'�ɂ���
��[��}]��[���f��]���t��(1/z)
- �C�Q�_�̋O�Ղ�ݒ�
��[Fig.4]�_A����ō��E�ɓ�����
- ����������ɂ́C�_����ʼnE�{�^�����N���b�N���u�_���̃L�[�{�[�h�ό`�v���g���ƕ֗�
��[Fig.5]�_�����~����œ�����
- �_�����~����ɐݒ肷��@��[�ҏW]��[�_(��������)](�_����I��)��[�~��ɂƂ�](�~��I��)
�����̑�������Ȃ��Ƃ�[Shift]�L�[�������Ȃ���}�E�X�œ_���ړ�������ƁC�ߐڂ����~(����)����ړ��\
�@����GC�̓l�b�g���[�N���ł̎g�p��ϋɓI�ɐ��i���Ă���C�g�p����p�\�R���Ɉˑ����Ȃ�Java�ō쐬�������@�[�W����������܂��D����ɂ��C�C���X�g�[����Ƃ�K�v�Ƃ��Ȃ��`�ł̗��p���\�ƂȂ��Ă��܂��D�p�\�R���ɃC���X�g�[������\�t�g�𐧌�����Ă���ꍇ�Ȃǂɂ����Ă��l�b�g���[�N��������ǂ̃p�\�R������ł�GC�����ƂŎg���܂��D�O�o�́uGC
Forum�v�ł́C�����ɑ̌��ł��܂��D
�@�܂�GC�̊�{�I�͑���ɂ��ẮC���̃��|�[�g�ɂ��Q�l�ɂ��Ă��������D
�@�@���uLet's enjoy using GC�v(������)�@�@http://www.nikonet.or.jp/spring/gc_ex/gc_ex.htm
2_2�@�O���t�\���\�t�g�uGrapes�v
2_2_1�y���@���z
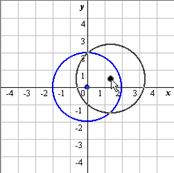
�@GRAPES�́C�p�\�R���̉�ʏ�ɗz���C�A���C�}��ϐ��\���̊�����ыɕ������̃O���t��`���C�����l�X�Ȋp�x���璲�ׂ邽�߂̃\�t�g�ł��D���ɕ�����₷�����[�U�[�C���^�[�t�F�C�X�ƁC�O���t��łׂ̍��Ȏw�肪�\�Ȃ��ߍ����\���͂������C��{�@�\�̏[���ƂƂ��Ƀv���[���e�[�V�����\�͂����ɍ����\�t�g�ł��D�ȉ��ɓ������܂Ƃ߂Ă����܂��D
- �z���C�A���C�}��ϐ��\���C�ɍ��W�̃O���t�̂ق��~�C�_�C�����C�����C�����`��\��j�_���璼���ւ̐����C�Q�_�����Ԑ���(����)�̕`��
- �}�E�X����ɂ��O���t(�_)�̈ړ��\
 �@�@
�@�@
- ���ׂĂ̐}�`�̓p�����[�^�Ǝc���@�\�̕��p�ɂ��O�Ղ�Ȑ��Q�̕`��\ �D�}�E�X�œ��������Ƃ��\�D�v���O�����i�X�N���v�g�j�Ńp�����[�^��c���̃R���g���[�����ł��C�O�Ղ̕`���J��Ԃ������������ōs�����Ƃ��ł���D
 �@�@
�@�@
- �Y�[���E���C�h�E�ړ��ȂǕ\���G���A�̃T�C�Y�����ł��ύX�\(�t���T�C�Y�\�����\)
- ���l��r�E��ϕ��ȂǁC�O���t�ׂ邽�߂̓���̏[��
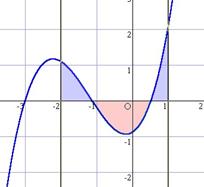 �@�@
�@�@
- �����@�\�������̒Ȃǂɗ��p�\
- ����ESAVE�ELOAD�Ȃǂ̕⏕�@�\�̏[��
- �}�E�X�ƃ��j���[�E�{�^���ɂ�钼���I�ŊȒP�ȑ���
- �����̋L�q�́C�ʏ�̋L�q�Ɠ����i��F��Z�L���̏ȗ��j
- �ꍇ�����̊����L�q�\
- �����̃T���v���f�[�^��p��(��360��)
2_2_2�@�y���ލ쐬��z
�@Grapes�́C��q����FunctionView�Ɠ��l�ɃO���t�`��c�[���Ƃ��āC���łɑS���I�ɗ��p����Ă���\�t�g�ł��D���̎��Ǝ��H���������\����Ă��܂��D���x���ւ̐����}���C�X�N���v�g�̎��s�ȂǍH�v����ʼn��ł��o���Ă��܂��̂�Grapes�̓����ł��D�X�N���v�g���g�����v���[���e�[�V�����^���ނ��쐬���Ă݂܂��傤�D
| �s��P�t�u�s�����̕\���̈�Ɖ��̎��������v |
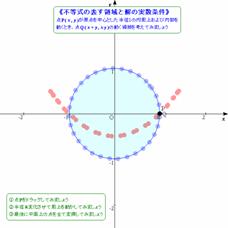
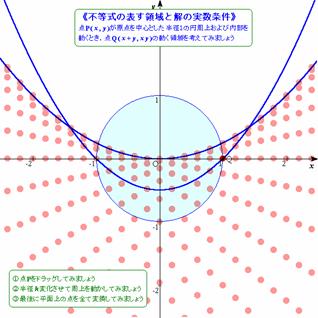
�@�u�_P(x , y)�����_�𒆐S�Ƃ������a�P�̉~�̎�����ѓ������Ƃ��C�_Q(x+y, xy)�̓����̈��}������v
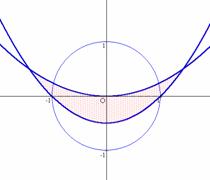 ���jx+y=u�Cxy=v�Ƃ����ƁC
���jx+y=u�Cxy=v�Ƃ����ƁC
�@x2+y2=u2-2v��1�c�@�C
�@t2-ut+v=0�̎����������D=u2-4v��0�c�A
�@����ċ��߂�̈�͉E�}�D
�@���k�͇@�͑��v�Ȃ̂ł����C�A�̎���������Y��邱�Ƃ������C�ux, y���ǂ�Ȏ������Ƃ��Ă��\������Ȃ�(u, v)������v�܂��́uu, v�������ł����Ă�x, y�������Ƃ͌���Ȃ��v�ȂǂƐ������Ă��ߑR�Ƃ��Ȃ��l�q�ł��D
�@To see is to believe.�@�A�̎����������C���[�W�����Ă݂܂��傤�D�V�����v�l�p�^�[����g�ɕt����ɂ͎��s���낪�K�v�ł��D���k�͋��t�̃V�i���I�ǂ���ɂ͗������Ă���܂���D
�@�p���ނ́u���ꂾ�I�v�Ǝv�����Ƃ���"�Z���Ԃō쐬�\"�ł��邱�Ƃ��d�v�ł��D���Ƃ̂Ȃ��Ő����Ԃ����g��Ȃ��v���[�����ނ𐔎��Ԃ������č쐬����̂ł́C����̋��ތ����ɋt���ʂɂȂ肩�˂܂���D�������Ԃ͒Z���Ԃłł��邱�Ƃɂ��������Ƃ͂���܂���D
�@Try and error�������ʂ��ݒ肵�Ă����Ƃ悢�ł��傤�D����ɂ�"�_�̃h���b�O"�𗘗p���܂��D
�@�ł́C�@�\���m�F���Ȃ������Ă݂܂��傤�D
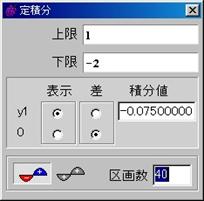
���쐬�菇�T�v��
- �h���b�O�\�ȓ_�o��ݒ肷��
���O���t�G���A�ʼnE�N�b���N����쐬
- �o��ϊ������_�p��ݒ肷��
- �P�ʉ~��`��
 �@
�@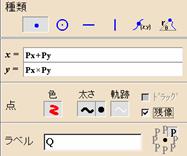
�@����ɁC���̉��ǂ������Ă݂܂��D
(a)�_P���ړ������𐧌�����
 ���h���b�O���[�h
���h���b�O���[�h
- ���������`�_P��y���W��"�{�P"�ƕ���������DGrapes�ł͕����t���l�܂��͐����Őݒ肳�ꂽ���W�����ւ��ރ��b�O�s�ɂȂ�܂��D
- ���������`�_P��x���W��"�{�P"�Ƃ���
- �� �� ��`x���W��1�Cy���W��'f (x)'�Ƃ��Ċ���`��f (x)���`����
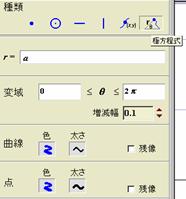 ���p�����[�^���g���ē�����
���p�����[�^���g���ē�����
- �p�����[�^���g��x�|y�������ɐ���
�`x���W�� a, y���W��b�ƃp�����[�^���g���Đݒ肷��D
- �~����ɐ���
�`�_�o�̃v���p�e�B�ŋɕ�������I������r= a
- �Ȑ���ɐ���
�`�h���b�O���[�h��'�Ȑ���'�Ɠ��l�ɂ���x���W��a�ɂ���
��������p�r�ɉ����Ďg�������Ă����܂��D
(b)�Q�_�̑Ή��W�����Ŗ�������
 �@�@
�@�@
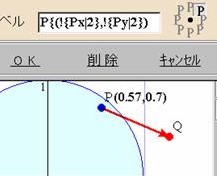 (c)�_P�̍��W�����x���ɕ\������
(c)�_P�̍��W�����x���ɕ\������
- ����\������ɂ́C���p������"{ }"�ň͂ށD
- ���𑽍����Ƃ��ĕ\������ɂ́C"?{ }"�ň͂ށD
- ���̒l��\��������ɂ́C�Ώێ���"!{ }"�ň͂ށD
- �\���������w�肷��ɂ́C!{��|����} �Ə����D
- �l�̕�����̏ꍇ�ɂ��\��������ɂ́C+!{��} �Ə����D
(d)�X�N���v�g�ɂ�鎩�����s
Grapes�̓����̈�ɂ��̊ȈՃX�N���v�g������܂��D������g���āu�s�����̕\���̈�Ɖ��̎��������v�̒p���ނ��쐬����Ǝ��̂悤�ɂȂ�܂��D
| �����G���A�ւ̋L�q���e�@�@//�Ŏn�܂镔���ͺ��ĕ� |
<B><L>�s�s�����̕\���̈�Ɖ��̎��������t</L></B>
�_{P(x,y)}�����_�𒆐S�Ƃ������a�P�̉~���エ��ѓ�����
�����Ƃ��C�_{Q(x+y,xy)}�̓����̈���l���Ă݂܂��傤
<Green>�@�_{P}���h���b�O���Ă݂܂��傤
�A���a{k}�ω������Ď�������Ă݂܂��傤
�B�Ō�ɕ��ʏ�̓_��S�ĕϊ����Ă݂܂��傤</Green>
#//������
#k := 1
#Px := 1
#Py := 0
#draw�@/�`��/
#ClrAimg�@//�c������
#-------------------------
#//�~�������(���a�Œ�)
#for t := 0 to 2 * Pi�@step 0.2
# Px := k * cos(t)
# Py := k * sin(t)
# draw
#next t
#t:=0
#Px:=k*cos(t)
#Py:=k*sin(t)
#draw
#------------------
#//�~�������(���aAuto)
#ClrAimg
#for k := 1 to 0.2 step -0.1
# for t :=0 to 6.28�@step 0.2
# Px := k * cos(t)
# Py := k * sin(t)
# draw
# next t
#next k
#Px := 1
#Py := 0
#draw
#------------------
#//���ʑS�̂�ϊ�����i��������j
#ClrAImg
#for t := 2.5 to -2.5step -0.2
# for s := 2.5 to -2.5 step -0.2
# Px := s
# Py := t
# draw
# next s
#next t
#Px :=1
#Py :=0
#draw
#---
#------------------
#//���ʑS�̂�ϊ�����i�����j
#ClrAImg
#for t := 3 to -2.5 step -0.2
# for s := 3 to -3 step -0.2
# Px := s
# Py := t
# calc�@//�`�悹���Ɍv�Z�̂�
# next s
# draw
#next t
#Px :=1
#Py :=0
#draw
#---
#HideScript�@//
#On k Change�@//�ϐ�k���ω������Ƃ����s����
#Px:=k
#Py:=0
 �@�@
�@�@
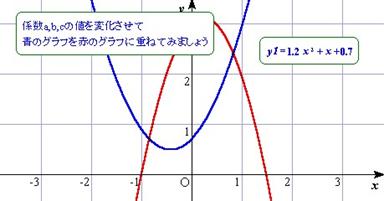
�@Grapes�̕\���͂̍����𗘗p����2�����̃O���t�̈�ʌ`�ł̌W���̈Ӗ����l����Q�[��������Ă݂܂��傤�D
| �s��Q�t �̌W����ω������ė^����ꂽ�������Ɉ�v������Q�[�� |
�@Grapes�ł́C�u�����v�@�\�Ő�����ϐ��̒l��\�������邱�Ƃ��\�ł��D�܂��C�f�[�^�p�l���̕����I�ȕ\���E��\�����\�ɂȂ��Ă��܂��D
���쐬�菇�T�v��
- �u����`�v�œ�������g(x) [��]�ƁC��f(x) [��]�̊����`����
���@f(x)= -2x^2+x+3, g(x)=ax^2+bx+c

- �⏕�Ƃ��Ċe�O���t��y�ؕЂƂ����ł̐ڐ�����͂���D���͌��\���ɂ���
 �@�@
�@�@
- �u�����v���ɖ��ƃO���t�̊������L�q����D���̂Ƃ�2�s�J����ƕʃ����Ƃ��Ĉ�����D
����������O���t�G���A�փh���b�O�����₷���ꏊ�Ɉړ�����D
 �@�@
�@�@ ��?{y1}�Ɠ��͂��邱�ƂŌW���ɐ��l��������"����"�Ƃ��ĕ\���ł��܂��D
��?{y1}�Ɠ��͂��邱�ƂŌW���ɐ��l��������"����"�Ƃ��ĕ\���ł��܂��D
- ���j���["�\��"��"����`�G���A"�C"������`�G���A"���\���ɐݒ肷��D
 �@�@
�@�@
2_3�@���O���t�\���\�t�g�uFunctionView�v
2_3_1�y���@���z
�@�O�o�́uGrapes�v�Ƃقړ��l�̋@�\�������Ȃ���C����Ɏ��̂悤�ȋ@�\������Ă��܂��D
- z=f(x,y)�ŕ\�����z���̋�Ԑ}�`��`��\
- ��͓I�\�������ł͂Ȃ��u�}�`�I�\���ɂ��_�̕\���E�`�悪�\�v
- �O�p�`�̂T�S�C�����̕��_�C�~����̓_�C�_�̉�]�C�Q�����̌�_�C�~�ƒ����̌�_�C�~�Ɖ~�̌�_
�~�O����̐ړ_�C�Q�~�̋��ʐړ_�C�����ւ̐����̑��C�����Ɋւ���Ώ̂ȓ_
- �u�g�ݍ��݃v���O�����v���p�ӂ���Ă���C���̐ݒ肾���ł����g����
- ��Ԑݒ�ɂ��ő�l�A�ŏ��l�̕\��
- ���ϕ��̃A�j���[�V����
�`���ϕω����̈Ӗ��ƋɌ��ɂ������W���̒�`
�`�ڐ��̕ω��ɂ�铱���̒�`
�`�敪���ςɂ���ϕ��ɒ�`�A�ő�a�A�ŏ��a�A��`�����A�V���v�\���̌���
�`��ϕ��Ɛϕ��@�̊�{�藝�̎��o���ƕ��ϒl�̒藝�̎��o��
�@��͓I�\������̂�Grapes��GC�̍�}�c�[���I�@�\��t�������O���t��}�c�[���Ƃ������\�t�g�ɂȂ��Ă��܂��D���̂��߁C���ލ쐬�ɂ����鎞�Ԃ��y������Ďg���₷���\�t�g�ɂȂ��Ă��܂��D
�@���̋@�\���g�������ލ쐬����Љ�܂��D
2_3_2�@�y���ލ쐬��z
| �s��P�t2��_A(0, 6)�CB(9, 0)�Ɖ~x2+y2=9�̎�����_�o������D���̂Ƃ��C��ABP�̏d�SG�̋O�Ղ����߂�D |
�@�ʏ킱�̋��ނł́�ABC�̏d�S��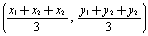 �Ȃǂ̂悤�ɉ�͓I�ɕ\�����Đݒ肷��K�v������܂����CFunctionView�ł́u��ABC�̏d�S�v�Ƃ����}�`�I�\�����\�ł��D
�Ȃǂ̂悤�ɉ�͓I�ɕ\�����Đݒ肷��K�v������܂����CFunctionView�ł́u��ABC�̏d�S�v�Ƃ����}�`�I�\�����\�ł��D
���쐬�菇�T�v��
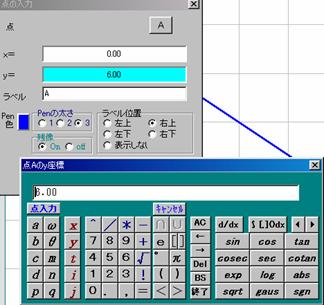
- 2��_A(0, 6)�CB(9, 0)���v���b�g����D���E�N���b�N������\
 �@�@
�@�@
- "�A��"�ʼn~��ݒ�@x2+y2=9
- �~����̓��_�o��ݒ�
�p�����[�^�["��"��p���܂��D
x���W�F3 cos (��)
y���W�F3 sin (��)
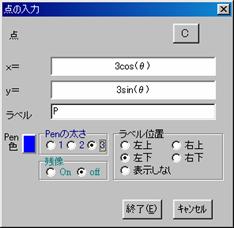
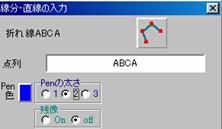
- "�����E�����E�~"�Ł�ABP��`��
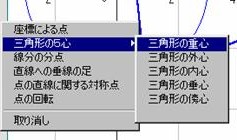
- �_�G���A�ʼnE�N���b�N�����ā�ABC�̏d�SG��ݒ肷��
- [�_�̖��O]�� G�C[���̒��_]��ABC�C[Pen�F]���ԁC[Pen�̑���]��3�@�C[�c��]��On�@�ɐݒ肵�܂��D
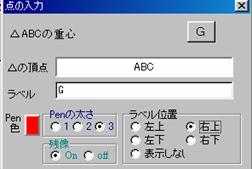 �@�@
�@�@
���v���[���e�[�V�����T�v��
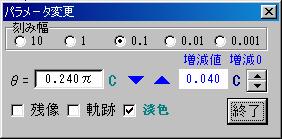
- Ҳ��ƭ�����[���Ұ��iP�j]�I������ƕ\�������u���Ұ��ύX���فv�ŃƂ̒l�����ē��_�o�����܂��D
[�c��]����������Əd�S�̕`���O�Ղ������яオ��܂��D
 �@�@
�@�@
�@�R�̃t���[�\�t�g�ɂ͂��ꂼ��̓���������܂����C�����̃\�t�g�ɋ��ʂ��Ă��邱�Ƃ͌���̎��ƂŔ|��ꂽ�ӌ����z���グ�āC���X�o�[�W�����A�b�v���d�˂Ă��邱�Ƃł��D�e�X�̍�҂Ƃ��Z��������钆�ł̍�Ƃ͕����̘J�͂ł͂Ȃ����ƂƎ@���h�ӂ�\���܂��D
�@���ތ����̍Œ��Ɂu������Ɛ��m�ɐ}(�O���t)��`���Ē��ׂ����v�Ƃ����v�������Ă���邱�Ƃ́C���Ƃ݂̂Ȃ炸�ʎw���̂Ƃ��ɂ��З͂����܂��D�܂��C����I�ȃv�����g���ލ쐬�̍ۂ��H�v����Ŏ�y�����m�Ȑ}(�O���t)��}���ł��܂��D�����x�C��߂ȃp�\�R���ɓ���Ďg���Ă݂Ă��������D
��TOP�@BACK�@NEXT��
 �u���Ɓv�ł̗��p�̂��߂̃\�t�g
�u���Ɓv�ł̗��p�̂��߂̃\�t�g �@
�@




 �i����P�j�u�_z����������Ƃ��̑�1/z�̋O�Ղ́v
�i����P�j�u�_z����������Ƃ��̑�1/z�̋O�Ղ́v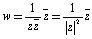 �̂悤�Ȑ����ł͂Ȃ��C���ۂɐ��k���g���_�������ƂŃC���[�W�����܂������Ƃ���ł��D�iFig.4�j
�̂悤�Ȑ����ł͂Ȃ��C���ۂɐ��k���g���_�������ƂŃC���[�W�����܂������Ƃ���ł��D�iFig.4�j �@�@
�@�@
 �@�@
�@�@
 �@�@
�@�@
 ���jx+y=u�Cxy=v�Ƃ����ƁC
���jx+y=u�Cxy=v�Ƃ����ƁC �@
�@
 ���h���b�O���[�h
���h���b�O���[�h
 ���p�����[�^���g���ē�����
���p�����[�^���g���ē�����
 �@�@
�@�@
 (c)�_P�̍��W�����x���ɕ\������
(c)�_P�̍��W�����x���ɕ\������
 �@�@
�@�@


 �@�@
�@�@
 �@�@
�@�@
 �@�@
�@�@
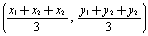 �Ȃǂ̂悤�ɉ�͓I�ɕ\�����Đݒ肷��K�v������܂����CFunctionView�ł́u��ABC�̏d�S�v�Ƃ����}�`�I�\�����\�ł��D
�Ȃǂ̂悤�ɉ�͓I�ɕ\�����Đݒ肷��K�v������܂����CFunctionView�ł́u��ABC�̏d�S�v�Ƃ����}�`�I�\�����\�ł��D �@�@
�@�@


 �@�@
�@�@
 �@�@
�@�@