��TOP�@NEXT��
1�@���w����ƃR���s���[�^�̊ւ��
1_1�@�R���s���[�^�����Ƃŗ��p����ړI
�@���w�̎��Ƃ̒��ŃR���s���[�^�����p���Ă���l�́C�����I�ɂ͂��������͂Ȃ��ƍl�����܂��B���̌����Ƃ��ẮC��{�I�ɕK�v�Ȃ��ƍl���Ă���C���ʓI���Ǝv���Ă��X�L�����s�����Ă���C�܂��̓X�L���͂����Ă���y�ɂł�������Ȃ��C�ȂǗl�X�Ȃ��̂��l�����܂��B
�@�܂��C�R���s���[�^�����Ƃɗp����Ƃ����Ă����̕��@�͐F�X����܂��B���ڐ��k������R���s���[�^�ɐG��đ��삷����̂��狳�t���p�Ƃ��Ďg�p������́C�X�ɂ̓v�����g�Ƃ��Ċ��p����ꍇ�ȂǗl�X�ł��B
�@�܂��C���̂��߂ɃR���s���[�^�𗘗p���邩�Ƃ�����{�I�ȉ��������������莝���Ƃ��厖���Ƃ����܂��B�R���s���[�^�����Ƃɗp�����{�I�ȗ��_�Ƃ��ẮC���̓_���l�����܂��B
- ���k�̎��Ɨ���x�����߂邽��
�������ނ̒��ɂ͔������ł͓`������Ȃ���ʂɑ������邱�Ƃ���������܂��B�Ⴆ�C�O���t��}�𑽂��p�����ނ�3������ԂȂǂł̓R���s���[�^�͌��ʓI�ł��B
- �����w�K�I�ȗv�f
�V�~�����[�V�����^�̃\�t�g��}�`��}�c�[���Ȃǂł́C�R���s���[�^��ʂ��ē���ꂽ�C���[�W��f�[�^���琔�w�I�ȍl�@���s�����Ƃ��\�ł��B
- �Ȋw�I�Ȏv�l�͂̈琬
���݁C���w�`�C�a�C�b�ɂ����ē�������Ă���A���S���Y���W�ł́C���w�I�ȗv�f��ʂ��ăR���s���[�^�̎d�g�݂�m��Ɠ����ɁC�Ȋw�I�Ȏv�l�͂̈琬��ڎw���Ă��܂��B
- ���k�ɐ��w�Ɋւ��鋻����S�����N���邽��
���Љ�̕ω��ɔ������w�̕K�v���������Ă��Ă���ɂ��ւ�炸�C���k�����̐��w���ꂪ�m���ɐi��ł��e�[�}���B�u���w�ɑ��鋻���E�S�v�̉��厖�Ɉ�ĂĂ����邱�Ƃ��厖�ł��B
- �l�b�g��ʂ������ތ���
�l�b�g��ɑ��݂���l�X�Ȑ��w�̑�ނׁC���w�ɐ��ޖ��͂�T�����邱�Ƃ��ł��܂��B
�@�����ł̓R���s���[�^�̊��p��Ƃ��āC�ǂ���������ʂłǂ̂悤�Ɏg�p���邱�Ƃ��ł���̂�����̗�����Ƃɍl���Ă݂����Ǝv���܂��B
1_2�@�����Ȋw�Ƃ��ẴR���s���[�^
�@���݂̃J���L�������ł͐��w�`�C�a�C�b�̂��ꂼ��ɁC���l���Z��A���S���Y�����������e�������Ă��܂��B�����������e�͐V���ȁu���v�ɂ�����u�A���S���Y���̊�b�v�Ƃ��d�Ȃ���e�ł��B�������������Ȋw�Ƃ��Ă̓��e��^���ʂ��爵�����H���l���Č��܂��傤�B
�@��̗�Ƃ��ăv���O���~���O����\�t�g�u�\�iBASIC�v��p�������H����Љ�܂��B�u�\�iBASIC�v�͕�����w����w���̔��Θa�v�搶���쐬�����t���[�̃\�t�g�ł��B�ڂ����͎��̃y�[�W���������������B
�@�@���u(����)�\�iBASIC�̃z�|���y�[�W�v
�@�@�@http://hp.vector.co.jp/authors/VA008683/
�@���ɏ\�iBASIC�����ƂŎg���Ƃ��̗��_�Ƃ��ẮC���̓_���������܂��B
- Windows95��œ����\�t�g�ł���B
- ���쌠�t���[�ł���B���̂��ߏ�ɍŐV�̃o�|�W�����Ŏg�p�ł���B
- ���Ɍy���C�\�t�g�̃C���X�g�|�����ȒP�BWindows�̃V�X�e����ύX���Ȃ��B
- ����ے��őz�肳��Ă��錾��BASIC�ɂقƂ�Nj߂��B
- �\�����v���O���~���O���\�B
- �G��`��p���ăO���t�B�b�N�̕ϊ����e�ՁB
- �G�f�B�^��ʁC�O���t�B�b�N�X��ʂȂǂ�������Ă��āC�ҏW�����₷���B
�@����ł͎��H�̎�ȗ�������Ă݂܂��傤�B
 ���I���W�i���̃e�L�X�g�����ƂɎ��{
���I���W�i���̃e�L�X�g�����ƂɎ��{
��ɂR�̕���C���Ȃ킿�C�v���O���~���O�̊�b�i�ϐ��Ǝ��C������E���͕��C�J��Ԃ������C�������f�C�z��ϐ��j�C�A���S���Y���̊�b�i�ő�E�ŏ��l�E���ϒl�C���בւ��C�����j�C�O���t�B�b�N�X�i�O���t�B�b�N�X�̊�b�C�Ȑ��̕`��C�}�`�̕ϊ��C���K�F�}�`�̕`��j���I���W�i���̃e�L�X�g�Ŏ��{�B
�����Ƃ̐i�ߕ�
- ���̐���
�ŏ��Ƀe�L�X�g�̗������t����������B�K�v�ɉ����āC���ł̐����C�f�B�X�v���C��ł̐����i��đ��M�j��^����B
- �ۑ�̉��K
����������C���k�͗��ɉ������ޑ�����s���B���t�͕K�v�ɉ����Ċ��ԏ������Ȃ���C���k�̎���ɓ�����B
- �ۑ�̒�o
�ۊO���I�������k�̓\�[�X�v���O�����������̃t�H���_�ɕۑ��B���̌�C���[���ō쐬�����t�@�C����Y�t���ċ��t���̎w�肵���A�h���X�܂ő��t����B���t�͑����Ă����ۑ���m�F���C�`�F�b�N����B
�����Ƃ̗l�q
- �e�L�X�g�̈ꕔ�����������Ƃ��������܂������C�قڗ\��ʂ�s���܂����B���Ƃ̗l�q�Ƃ��ẮC���̂悤�Ȋ����ł����B
- �ŏ��̓p�\�R���������{����̓��[���[�̑���Ɋ���Ȃ����k�����Ȃ�������Ă������C����ɏK�����Ă������B
- ���ԏ������㔼�ɂȂ�Ǝ�������Ȃ��Ȃ�C�ۑ�����Ȃ��̂Ɉꐶ�����ł������B
- ����̉ۑ�������ł����ɐi�x�ɒǂ����Ă���Ȃ����k�������B�����������k�͋x�ݎ��Ԃɑ��߂ɗ��āC�ۑ�쐬�Ɏ��g��ł����B
- ���k�Ԃ̔\�͊i�����傫���C��l�łǂ�ǂ��ɐi�ސ��k�Ɩ���̉ۑ�������ł��Ȃ����k�̊i���͑傫�������B���̂��߁C�p�\�R���ɑ��鋻���E�S�x�������o�āC�����������k�C���������k�����܂�Ă����B
- �Ō�̎��R�ۑ�ł͎����̃A�C�f�B�A�Ɨ͗ʂƂ𑊒k���Ȃ���C�l�X�ȃ��j�[�N�ȍ�i����������ꂽ�B
- �ۑ���Ƃ��烁�[���ő����Ă��鐶�k�������B�܂��C�\�iBASIC�̃\�t�g���t���b�s�[�ɃR�s�[�������k��30���ȏア���B
���@���k��i��@��
���]�����ɂ���
�v���O���~���O�̊�b��A���S���Y���̊�b�ɂ�������ɂ��ẮC����܂ł����������Ă��܂����B���ے��ɐ��w�ɂ����Ă��]�����Ƃ��Ă͂�����x�蒅���Ă���Ƃ����܂��B����̓O���t�B�b�N�W�̕�����]�����Ɏ�����Ă݂܂����B�ڂ����͎��̃y�[�W���������������B
�@�@���u�V���ȁu���v�b�f����ɂ�����u���w�v�v
�@�@�@http://www.nikonet.or.jp/spring/cg/cg.htm
|
���̃v���O�����͉���(1)�`(3)�̒�����`�悷����̂ł���B���ꂼ��̃O���t�ɑ��āC�߂�B�������CPLOT LINES : x1 ,y1 ; x2 ,y2 �ŁC2�_(x1 ,y1), (x2 ,y2)������Ō��Ԃ��̂Ƃ���B

SET WINDOW -3,9,-1,16
DRAW AXES
LET Y=0
FOR I=1 TO 5

PLOT LINES : 0,Y;5,Y
NEXT I
END
|
�@�@���u�\�iBASIC��p�����v���O���~���O�̎w���v�i���c��j�j
�@�@�@http://www.nikonet.or.jp/spring/program/program.htm
�@�x�썂�Z�̏��}���搶���\�iBASIC��p�������l�̎��H���s���Ă��܂��̂ŁC���̃y�[�W���������������B
�@�@���u���w�I�������S�̐��w���ށv�i���}���@�߁j
�@�@�@http://www.nikonet.or.jp/spring/kyouzai/kyouzai.htm
1_3�@�����w�K�Ƃ��ẴR���s���[�^
�@���w�̎��Ƃ̈ꕔ���ɂ����Đ��k������R���s���[�^�𑀍삵�C���w�̑�ނ�����l���Ă����C����Ȋ��p�@���������Љ�܂��傤�B
�@�܂��͊��O���t�\���\�t�g�uGrapes�v��p�������H�ł��B���̃\�t�g�͑�㋳���w�t�������w�Z�r�c�Z�ɂ̗F�c���v�搶��������t���[�E�F�A�ŁC���̂悤�ȗl�X�ȓ���������܂��B
- �C���^�[�l�b�g�Ń_�E�����|�h�ł���t���[�E�G�A�ł���B
- Delphi�ō쐬����Ă��邽�ߎ��s�t�@�C���݂̂œ��삷��B
- �T�C�Y���������t���b�s�[�ꖇ�Ɏ��܂�B
- �z���C�A���C�ɕ������C�s�����̕\���̈�Ȃǂ��T�|�|�g�B
- �p�����[�^��ω������邱�ƂŃO���t�̕ω����ǂݎ���B
- �c���\����X�N���v�g�ŃA�j���[�V�������ł���B
�@���̃\�t�g��p����2�����̎��H����Љ�܂��B
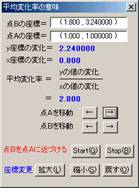
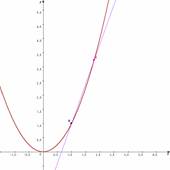
��2�����̎��̌`����ʌ`�����ɓ���
��ʌ`�̎����ɗ^���p�����[�^�̕ω��k�ɍl�@�����܂����B��ʓI�Ȍ`���瓱�����������莩�R�ŁC���Ƀp�����[�^b�̖��������k�ɖ��ӎ����������܂��B�W���`�ł̓����̒P���������������Ƃɂ��C�W���`�̏d�v�������o�Ƃ��Ă킩��܂��B
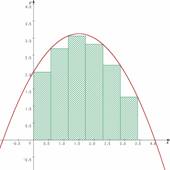
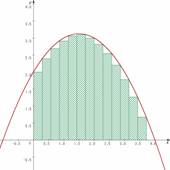
���쐬�����摜�����[�v���ɂ܂Ƃ߂�Ƃ���"���K���o"
�p�����[�^��ς��ē�����O���t��Grapes�ォ��R�s�[���C���[�v���ɓ\��t����Ƃ�����Ƃ������܂����B�Ō�Ɋe�p�����[�^�̉ʂ����������l�@�����C�v�����g���o�����܂����B
��2�����̈�ʌ`�̃p�����[�^b�̐����̕⑫�Ɂu�a���v�Ƃ��ẴC���[�W��
2�����̈�ʌ`�̃p�����[�^b�̎��Ӗ��͂Ȃ��Ȃ�����Ƃ���ł����C�������ŎD�y�V�썂�Z�̒������������\���ꂽ�u�a���v�̍l������⑫�Ƃ��Đ������܂����B
�@�@���u�a���Ƃ��Ă̂Q�����̃O���t�v�i���������j
�@�@�@http://www.nikonet.or.jp/spring /add/add.htm
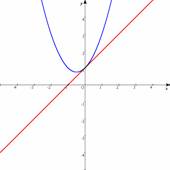
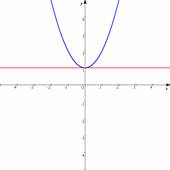
y��ax2�{bx�{c�̃O���t��y��ax2��y��bx�{c�̃O���t�̘a���Ƃ��čl���Cy����̐ؕ�c��y��bx�{c�̒����ɐڂ���Ƃ������Ƃ��C�p�\�R���Ńp�����[�^��ς��Ȃ�����܂��B
�@���H��ɂ��Ă̏ڍׂ́C���̃y�[�W���������������B
�@�@���u2�����̓��������ɂ�����R���s���[�^�̊��p�v�i���c��j�j
�@�@�@http://www.nikonet.or.jp/spring/gp_ft/gp_ft.htm
�@�܂��C�D�y��k���Z�̎����搶���C�u�~�ƒ����v�u���낢��ȋȐ��v�u�s�����̕\���̈�v�ɂ�����Grapes��p�������H������Ă��܂��̂ŁC��������������������B
�@���u�R���s���[�^���p�̎��ƕv�i������v�j
�@�@�@http://www.nikonet.or.jp/spring/cp_rpt/cp_rpt.htm
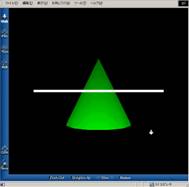
�@���ɁC����s�����̍쐬�����t���[�\�t�g�uVirtual Solid�v��p���āC��Ԑ}�`�̒f�ʐ}��W�J�}�w���ł̎��H���l���Č��܂��傤�B���̃\�t�g��Version1.00�Ɍ���t���[�̃\�t�g�ŁC���̂Q�̓_�ɓ��������t���[�\�t�g�ł��B
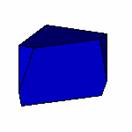
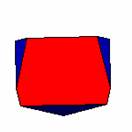
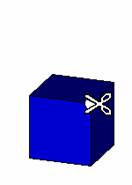
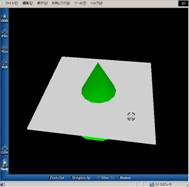
����Ԑ}�`�̐ؒf
���̏�̂R�������w�肷�邱�Ƃɂ��C�C�ӂ̈ʒu�Ő}�`��ؒf�ł��܂��B�ؒf�͈�x�����łȂ����x�ł����s�ł��܂��B�܂��C�ؒf�������̂��ォ��W�J���邱�Ƃ��ł��܂��B
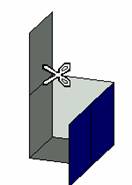
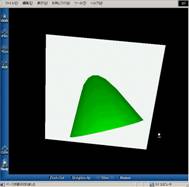
����Ԑ}�`�̓W�J
���̂�C�ӂ̌`�ɓW�J�ł��܂��B�W�J��C���_��ӂ��ǂ̂悤�ɐڂ��Ă������ׂ邱�Ƃ��ł��܂��B
�@���p�\�ȗ��̂Ƃ��ẮC�S�Ă̐����ʑ́E�p���E�p���E��������܂��B�܂��C���̖̂ʂ��ƂɎ��R�ȐF�����蓖�Ă���C�ؒf�ʂ�^���ʂ��猩�邱�Ƃ��ł���Ȃǂ̍H�v���Ȃ���Ă��܂��B��Ԑ}�`�̓��������ɂ����āC�����̂̓W�J��ؒf�ʂ̊w�K�ɑ�ϖ��ɗ����܂��B���w�Z���w�N���瓱���������e�ł����C���݂̐��k�ɂƂ��Ă͂���������Ԕc���͂ƂĂ����ȕ���̂悤�ł��B���ɓW�J���ؒf���P�P��ނ��邱�Ƃ���i�ؒf�ʂœ��r��`������ƂP�Q��ށj�C�S�Ă̏ꍇ�k�ɔ��������邱�Ƃ͂��Ȃ荢��ȏł��B�ƂĂ��P���Ԃł͂��Ȃ�����Ȃ��ۑ肩������܂���B�Ō�ɉƂ��Ĕz�z�����v�����g���C���̃y�[�W�ɂ���̂ŎQ�l�ɂ��Ă��������B
�@�@���u���w�ʎ蔠�@�����̂̓W�J�E�ؒf�v�i���c��j�j
�@�@�@http://www.nikonet.or.jp/spring/sanae/MathTopic/MathTopic.htm
1_4�@�p���ނƂ��ẴR���s���[�^
�@���Ɏ��Ƃɂ�����p���ނƂ��Ă̊��p�@���C�������̋�̗�����Ƃɍl���Ă݂܂��傤�B�\��LAN�������i�ޒ��C�v���W�F�N�^��p�����u����^�v�u���^�v�ł̗��p�����ꂩ��̃R���s���[�^���p�̒��S�ƂȂ邱�Ƃ͖��炩�ł��傤�B�p���ނƂ��Ă̊��p�͗l�X�ȑ�ނ��l�����܂��B���̂����̂ق�̂��������Љ�܂��B
�@�܂��C���O���t�\���\�t�g�uFunctionView�v��p�������p����Љ�܂��B���̃\�t�g�͌Q�n�����ː��H�ƍ��Z�̘a�c�[���搶���쐬���ꂽ�t���[�E�F�A�̃\�t�g�ł��B�p�C�v�����g���ނɂ�����O���t�쐬�̂ق��C�Ĕz�z�t���[�̂��ߑS�Ẵp�\�R���ɃC���X�g�[�����Đ��k�ɖ������̏�ʂő��삳���邱�Ƃ��\�ł��B����Ŏ��Ƃ�S�����鍂�Z���w���t���쐬�����v���O�����ׁ̈C���ۂ̎��Ƃ�z�肵���@�\���ŏ����������Ă���C�A�j���[�V�����Ȃǂ̍쐬���ȒP�ɂł���Ƃ��낪�ő�̖��͂��Ƃ����܂��B���ɂ�����̂͐ڐ��̕ω��C���ϕω����Ɋւ��鋳�ނł����C���������p�̋��ލ쐬�ł́CFunctionView�͑傫�ȈЗ͂�����Ƃ����܂��B
�@�@���u���T���ɂ�����p���ށE��{��v�i���c��j�j
�@�@�@http://www.nikonet.or.jp/spring/ft_pre/ft_pre.htm
�@�@���u�y���K�z���Z���w�x���c�[���u���O���t�\���\�t�g�v�v�i�������j
�@�@�@http://www.nikonet.or.jp/spring/Fview/Fview.htm
�@�\��LAN�����ɔ����������ɂ��C���^�[�l�b�g�����������Ƃ��l����C�l�b�g��Ńu���E�Y�ł��鋳�ނ͑�ϖ��͂�����܂��B����ȋ��ނ�VRML��Java�̂Q���ɂƂ��čl���Č��܂��B
�@�܂�VRML��p�����p���ނ̍쐬��ł��BVRML(Virtual Reality Modeling Language)��HTML�̂R�����łł���C�C���^�[�l�b�g��ŃT�C�o�[�X�y�[�X���\�z���邽�߂̌���ł��B����Ƃ����Ă��b�⑼�̃R���s���[�^����̂悤�ȃv���O���~���O����ł͂Ȃ��C"�V�[���L�q����"�Ƃ����܂��BVRML�̃C���[�W�́C�܂���̕��i�i�V�[���j������C���̒��ɂ������̃I�u�W�F�N�g�i�m�[�h�Ƃ����j���z�u�����C�Ƃ������Ƃ���ł��傤���BVRML�t�@�C���̓R���s���[�^�ɗ����\�ȃI�u�W�F�N�g�̏W���ɕϊ������ʏ�ɕ\������܂��B�܂�C�v���b�g�z�[���ɓƗ��Ȃ̂ł��B
�@�܂��ɃR���s���[�^�O���t�B�b�N�X�����ɓ����������̂ŁC�L�x�ȃ��f����e�Ղɐ������邱�Ƃ��ł���g�ݍ��@�\�𑽂������Ă��܂��B�Ȃɂ��e�L�X�g�x�[�X�ō쐬���C�ǂ݂Ƃ�\�ȃu���E�U������C�����ɕ\���ł���Ƃ��낪��y�Ŏg���₷���Ƃ����܂��B
�@��̗�Ŏ����܂��傤�B���̗�͉~���Ȑ����C���[�W�����������̂ł��B
�@�@���uVRML2.0 TUTORIAL�v�i���c��j�j
�@�@�@http://www.nikonet.or.jp/spring/sanae/VRML2/Vrml2.htm
�@�@���uLet's Create The 3D Graphics�v�i���c��j�j
�@�@�@http://www.nikonet.or.jp/spring/Ma_VRML/Ma_VRML.htm
�@����Java�A�v���b�g��p�������ލ쐬����Љ�܂��B�v���O���~���O����Java�̓������܂��ɗ���Ǝ��̂悤�ɂȂ�܂��B
- Architecture Newtral
Java���ɂ����ẮC�e�A�v���b�g��Java Virtual Machine�Ƃ������z�̃R���s���[�^��œ��삵�܂��B���̂��߁C�@���OS�ɊW�Ȃ����̂܂ܗ��p�ł��܂��B
- static����interactive��
�T�[�o�[���K�v�ȃv���O�������C�����̃u���E�U��œ��삳���邱�Ƃ��\�ł��B
- object�u���Cclass�p��
�v���O�����m���C�����Ċȑf�����鎖���ł��C�v���O�����̍ė��p��Ǘ��E�J�����e�ՂɂȂ�܂����B
- byte type
Java�͒��ڃ�������ɏ������܂Ȃ����߂ɁC���Ɉ��S���������BJava���̂̓A�v���P�[�V�����쐬�̌���Ƃ��Ă��p���邱�Ƃ��ł��邽�߁C����p�̌���Ƃ��Ẳ\������߂Ă��܂��B
�@��̗�����Ƃ�Java�A�v���b�g��p�������ޗ�����Ă݂܂��傤�B���̗�́C��p�f�Ƃ��Ă̍s��̖������p�����[�^�̕ω��ƂƂ��ɍl����������̂ł��B�Ώ̈ړ��C�g��E�k���C���炵�ϊ��C��]�ړ��C�މ�����ϊ��Ȃǂ̊�{�I�ȕϊ��ƍs�ǂ̂悤�ȊW�����邩�����邱�Ƃ��ł��܂��B�X�ɂ͕��f�ϊ��Ƃ̊W�ɂ܂Ŕ��W�����čl�������܂��B�܂�肭�ǂ��������g�߂ȉ摜��ϊ������邱�ƂŃC���[�W�ł��₷���Ȃ�܂��B
�@�@���uJava��1���ϊ��v�i���c��j�j
�@�@�@http://www.nikonet.or.jp/spring/transfer/transfer.html
�@���̗�͂��낢��ȋȐ����p�����[�^��ω������邱�ƂŁC�ǂ̂悤�ɕω����邩���l�@���邽�߂̂��̂ł��B
�@�@���uJava�ł݂邢�낢��ȋȐ��v�i���c��j�j
�@�@�@http://www.nikonet.or.jp/spring/sanae/Curves/Curves.htm
1_5�@���ލ쐬�Ƃ��ẴR���s���[�^
�@���ȏ��ł͒��ڈ���Ȃ��悤�Ȃ��̂ł��C���e�I�ɖʔ�����ΐ��k�͊S�������܂��B���ɍŋ߂̐��k�̌X���Ƃ��Ă͐}��O���t�Ȃǂ̃C���[�W���痝�����Ă����X���������܂��B���̂��߁C���w�ʐM��v�����g�Ȃǂ̕⏕�I�ȃv�����g�Ɏ��o�I�ȃC���[�W�}�Ȃǂ��쐬���đ}�����邱�Ƃ͑�ό��ʓI�ł��B���ڎ��Ƃɂ����ăR���s���[�^���g�p����킯�ł͂���܂��C���ލ쐬�̈���@�Ƃ��āC���ɃC���[�W�}�쐬�̂��߂ɃR���s���[�^�����p���邱�ƂŐ��k�̗���x�̎菕���Ƃ��邱�Ƃ��ł��܂��B��̗�Ƃ���Web�^���w�ʐM�u���w�ʎ蔠�v�̒����炢�������Ă݂܂��傤�B
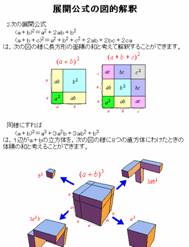
- �W�J�����̐}�I����
(a�{b)3�̓W�J�������C1�ӂ�a�{b�̗����̂�8�̒����̂ɂ킯���Ƃ��̑̐ς̘a�ƍl��Visual�ɐ�������B
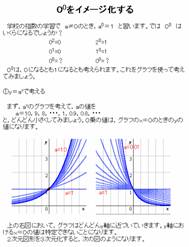
- 00���C���[�W������
�w���̊w�K��a��0�̂Ƃ�a0��1�ƏK�����C�ł�00�͂�����ɂȂ�̂ł��낤�B3�����}�`�����Ƃ�Visual�ɐ�������B
- �g�ʂɂ݂�2���Ȑ�
�r�ɏ��𓊂����ꂽ�Ƃ��ɂł���g�ʁB���̒��ɉB��Ă���2���Ȑ����l����B
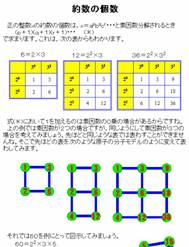
- �̌�
���̐���x��apbqcr����̖̌���(p�{1)(q�{1)(r�{1)�c�ŋ��܂邪�C�����3�������q���f�����g���Đ�������B
- �����̌����̎��o��
�O�p���̍����̌����̈Ӗ����C�x�N�g����p���Ď��o�I�ɐ�������B
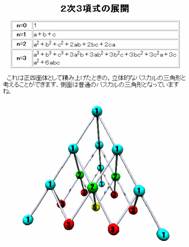
- 2��3�����̓W�J
(a�{b)n�̓W�J���Ɍ����p�X�J���̎O�p�`�B�����(a�{b�{c)n�܂Ŋg�����C���̓I�ȃp�X�J���̎O�p�`�����������B
�@�@���u���w�ʎ蔠�v�i���c��j�j
�@�@�@http://www.nikonet.or.jp/spring/sanae/MathTopic/MathTopic.htm
1_6�@���ތ����Ƃ��ẴR���s���[�^
�@�u���w������H������v�ł͓���I�Ȏ��Ƃ̎��H�ɖ𗧂�����ڎw���Ċ������Ă��܂����B���̒��ōł������I�Ȃ̂́C���C�Ȃ���̃e�[�}���C�l�X�Ȋϓ_����H����[�߂Ă������Ƃ����_�ł��B�����������ތ����̒��ł��R���s���[�^�͑傫�ȈЗ͂����܂��B��̗��2�قǏЉ�܂��傤�B
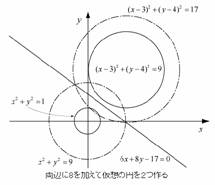
�@�܂���ڂ͑��⍂�Z�̒��������搶����N�����u2�~�̌�_��ʂ钼���̖��v�ł��B
�w2�̉~
�@�@�@x2�{y2��1 �c�@�Cx2�{y2�|6x�|8y�{16��0 �c�A
�@�̌�_��ʂ钼���͉���
�Ƃ��������C�@�|�A��� 6x�{8y�|17��0�Ƃ��Ă��܂��̂́C�e�N�j�b�N�Ώd�̎��w�̍ł�����̂ł���B�x
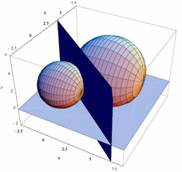
�@���̃e�[�}�����ƂɁC�x�L�̔�Ƃ��Ă̓_�̋O�Ղ⋅����xy���ʂƂ̌���肪���Ȑ��Ȃǂ̕��͂��Ȃ���܂����B�X�ɐ��E�f���ɂ܂ōL���C���~�̌�_�̉e�Ƃ��Ă̒����̑��݂������܂����B�����������ތ����ɂ��R���s���[�^�͖{���ɑ傫�ȈЗ͂����܂��B����l�̗͂����ł͂Ȃ����Ȃ����E���R���s���[�^�͍��o���Ă����̂ł��B
�@�܂��C�h���I�Ɂu���w�v�Ƃ͉����낤���C�Ƃ������_�c�����[�����O���X�g��ł�����܂����B�Q���҂����Z������Љ�l�܂łɎ���C�e�[�}�ɂ���Ă͕��́E�c�_���̂���̋��ނƂȂ肤�邱�Ƃ��������̂ł��B����������@���\�ɂ����̂̓��[�����O���X�g���܂߂��}�̂Ƃ��Ẵ��[����Web�R���e���c�Ƃ��������f�B�A�̑��݂��������܂��B
�@�Ȃ��C���̃e�[�}�ɉ�������A�̃��|�[�g���C���̃y�[�W�ɂ���܂��̂ŎQ�l�ɂ��Ă��������B
�@�@���u2�~�̌�_��ʂ钼���̖��v
�@�@�@http://www.nikonet.or.jp/spring/thema/d_circle.htm
�@���ɕ��f���ɂ��}�`�ϊ���"��p�f"�Ƃ��Ă̊ϓ_����A�v���[�`�����݂����ޗ���Љ�܂��B���s�ے��ł͉Ȗځu���wB�v�́u���f���ƕ��f�����ʁv�ň�������e�ł��B���f���ʏ�ɂ�����}�`���̉�@�ɂ́C�l�X�Ȗʔ����v�f���܂�ł��܂����C�@�B�I�Ȍv�Z�ɂ���Ă��̖��͂����킹�Ă����@���ڗ����܂��B������ł͂��̃e�[�}���X�ɐ[�߁C������₷���C���[�W�����Ă��܂����B�����������f�ϊ���`�悷��̂ɏ\�iBASIC�͍œK�ł��B����͓Ǝ��̊g���@�\�Ƃ��ĕ��f�����[�h�������Ă��邩��ł��B�v���O�����̏����� OPTION ARITHMETIC COMPLEX �Ɛ錾����ƁC���f�����[�h�ɐݒ肳��܂��B�����āCz=complex(x,y)��z=x+iy�Ƃ������f���������C�����`���邾���ŕϊ���̕��f����������̂ł��B���̌�Re(w)�CIm(w)�Ƃ��āC�����Ƌ����̕��������o���`�悵�܂��B���̐}��w=z2�ϊ� �ʼnƁC�ԁC�ۂ��ꂼ���ϊ����ē���ꂽ�}�ł��B�ł��傫�ȓ����̓}�E�X�y����"�Ȃ���"���ƂŁC�ϊ���̐}�`���p���������߁C�V�~�����[�V�����Ƃ��Ẳ��l���傫�����Ƃł��B
�@���̐}�͕ϊ��̊���ς��Ď����Ă݂����̂ł��B
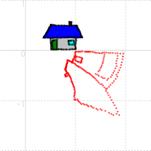 |  |  |
| w=1/z�̕ϊ� | w=��z�̕ϊ� | w=ez�̕ϊ� |
�@�@���u��p�f�Ƃ��Ă̕��f���v
�@�@�@http://www.nikonet.or.jp/spring/thema/complex.htm
1_7�@�l�b�g���[�N�Ƃ��ẴR���s���[�^
 �@�k�������Z����ł�'97�N����l�b�g���[�N�^�̋��ރf�[�^�x�|�X�u���w�̂����݁v�����J���Ă��܂��B���w�ɂ܂��b����W�߂��u���w�g�s�b�N�X�v�C���i�̎��Ǝ��H�̕�����߂��u���H�L�^�E���|�[�g�v�C�e�[�}���i���Č�����[�߂Ă����u�e�[�}�ʋ��������v�Ȃǂ�����܂��B�܂��C�n��̍��Z���̐��w�̎�������̂��߂ɒ��N���{���Ă��Ă���u�k�C�������w�Z���w�R���e�X�g�v�̖��Ⓑ�N�~�ς��ꂽ���ŃV���[�Y�����ꂽ�u���w�̏���Z�v�u���C���鐔�w�v�u���w�ʎ蔠�v�Ȃǂ��V���ɉ����܂����B
�@�k�������Z����ł�'97�N����l�b�g���[�N�^�̋��ރf�[�^�x�|�X�u���w�̂����݁v�����J���Ă��܂��B���w�ɂ܂��b����W�߂��u���w�g�s�b�N�X�v�C���i�̎��Ǝ��H�̕�����߂��u���H�L�^�E���|�[�g�v�C�e�[�}���i���Č�����[�߂Ă����u�e�[�}�ʋ��������v�Ȃǂ�����܂��B�܂��C�n��̍��Z���̐��w�̎�������̂��߂ɒ��N���{���Ă��Ă���u�k�C�������w�Z���w�R���e�X�g�v�̖��Ⓑ�N�~�ς��ꂽ���ŃV���[�Y�����ꂽ�u���w�̏���Z�v�u���C���鐔�w�v�u���w�ʎ蔠�v�Ȃǂ��V���ɉ����܂����B
�@�u���w�̂����݁v���ڕW�Ƃ��Ă���̂́u���J�v�u�A�g�v�u�~�ρv�̂R�ł��B�����Ă��̂R�����ƂȂ�C�P�Ȃ錤����̌��J�y�[�W�ɂƂǂ܂�Ȃ��C��萔�w����ɍ��������y�[�W�ɂ������ƍl���Ă��܂��B�N����킸�����̈ӌ������C�����Ȏ��݂����N�̒~�ςƓ����ɐ��w����ɏ��Ȃ��炸������S�����Ƃ��ł���܂łɂȂ��Ă��܂����B�Z��LAN�������i�ޒ��ŁC�����ƂɎg���鋳�ލ��̒~�ς����߂��Ă��܂��B����܂Œ~�ς��ꂽ�f�[�^���C�X�ɂ�茻��ɑ������`�ł̊Ҍ��̎d�����K�v�ƂȂ�ł��傤�B
�@�@���l�b�g���[�N�^�̋��ރf�[�^�x�|�X�u���w�̂����݁v
�@�@�@http://www.nikonet.or.jp/spring/
1_8�@���͂���ʂłȂ��R���s���[�^�@�`�����܂ł����ނ����S
�@����܂Ō��Ă����悤�ɃR���s���[�^��l�X�Ȍ`�Ő��w����ɗp���邱�Ƃ��ł��܂��B�������C�ǂ�Ȍ`�ŗp�����Ƃ��Ă��厖�Ȃ̂͋��ނ̒��g�ł��B���͂�����Ƃ����ɂ́C���͂����ނ��K�v�ɂȂ�܂��B�\�t�g�E�G�A�̋@�\�𗝉����Ďg�����Ȃ��O�ɁC�ǂ���������ʂŁC�ǂ�ȓ��e�ŗp�������̂��B�����������ތ����������K�v�ł���Ǝv���܂��B
�@�R���s���[�^����ɗ���̂��傫�Ȗ�肪����܂��B�ŋ߂̐��k�̓R���s���[�^�Ɋ���Ă��鐢��ł�����C���e�������Ă��Ȃ�������C���炾��Ɗԉ��т������Ƃł͂����ۂ������Ă��܂��܂��B��ʂɂ���ẮC�l�X�ȋ����p���Đ���������C���K�`���̎��Ƃ������ꂽ�����C�t�ɐ��k�ɂƂ��Ă͐V�N�ŁC���C�C���p�N�g�������Ƃ����܂��B�܂��C���w�ʐM��C���[�W�摜�𑽂������ꂽ�v�����g�Ȃǂ����ʂ�����Ƃ����܂��B
��TOP�@NEXT��
 ���I���W�i���̃e�L�X�g�����ƂɎ��{
���I���W�i���̃e�L�X�g�����ƂɎ��{























 �@�k�������Z����ł�'97�N����l�b�g���[�N�^�̋��ރf�[�^�x�|�X�u���w�̂����݁v�����J���Ă��܂��B���w�ɂ܂��b����W�߂��u���w�g�s�b�N�X�v�C���i�̎��Ǝ��H�̕�����߂��u���H�L�^�E���|�[�g�v�C�e�[�}���i���Č�����[�߂Ă����u�e�[�}�ʋ��������v�Ȃǂ�����܂��B�܂��C�n��̍��Z���̐��w�̎�������̂��߂ɒ��N���{���Ă��Ă���u�k�C�������w�Z���w�R���e�X�g�v�̖��Ⓑ�N�~�ς��ꂽ���ŃV���[�Y�����ꂽ�u���w�̏���Z�v�u���C���鐔�w�v�u���w�ʎ蔠�v�Ȃǂ��V���ɉ����܂����B
�@�k�������Z����ł�'97�N����l�b�g���[�N�^�̋��ރf�[�^�x�|�X�u���w�̂����݁v�����J���Ă��܂��B���w�ɂ܂��b����W�߂��u���w�g�s�b�N�X�v�C���i�̎��Ǝ��H�̕�����߂��u���H�L�^�E���|�[�g�v�C�e�[�}���i���Č�����[�߂Ă����u�e�[�}�ʋ��������v�Ȃǂ�����܂��B�܂��C�n��̍��Z���̐��w�̎�������̂��߂ɒ��N���{���Ă��Ă���u�k�C�������w�Z���w�R���e�X�g�v�̖��Ⓑ�N�~�ς��ꂽ���ŃV���[�Y�����ꂽ�u���w�̏���Z�v�u���C���鐔�w�v�u���w�ʎ蔠�v�Ȃǂ��V���ɉ����܂����B