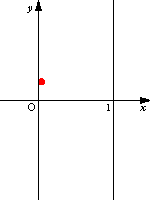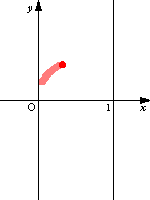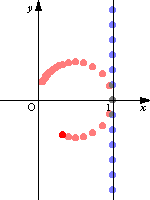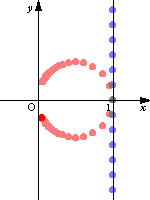
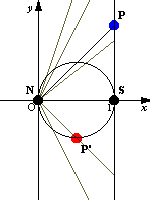
青い点が原像 赤い点が変換された像

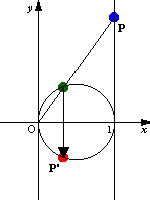
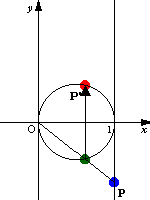
　これはN極を原点，S極を1だと考え，NSを直径とする円を考えれば説明がつく．直線上の動点PとN極（原点）とを結ぶ線分と円との交点を，実軸に関して対称に折り返した点が1/zによる像P'となる．この実軸に関して対称に折り返すことで，ねじれのような状態が生じている．

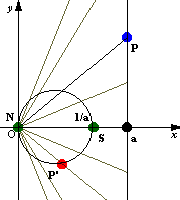
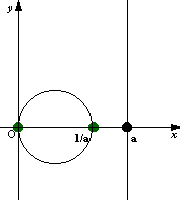
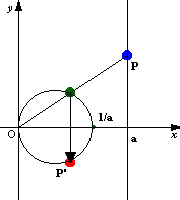
　同様にして実軸に垂直でaを通る直線z(a)を変換させて見る．先ほどと同様にN極を原点にとる．また，原点から最も近い点aを変換した点1/aをS極ととればよい．つまり直線の変換された像は，原点と1/aを直径とする円と考えられる．また，点Pの像は原点と結んだ線分と円との交点を実軸に対象に折り返した点である．

　先ほどのリーマン球面との対応で示したように，
　　　　原点の反転が∞，∞の反転が0
　　　　原点からの距離が最小な点の反転は，原点からの距離が最大
と考えるのである．