 |
 |
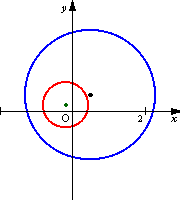 |
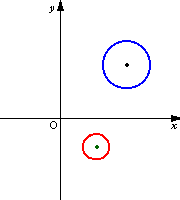
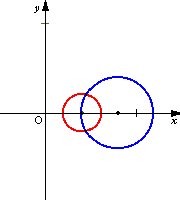
次の図は原像の円の中心を固定して半径を大きくしていったときの,変換される円の軌跡を表したものである.次第に変換される円の半径が大きくなり,原像が原点を通るときに直線となり,次に反対側にまた円が現れてくるのが分かる.
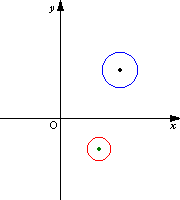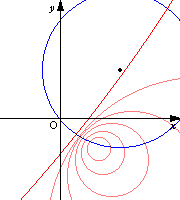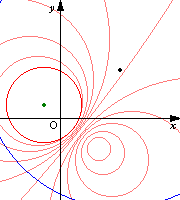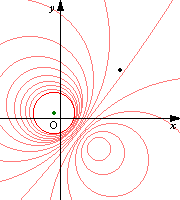 |
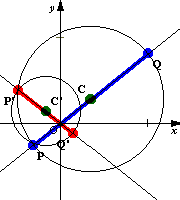
青い線が原像 赤い線が変換された像 |
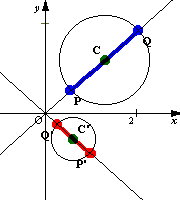
さて変換されたあとの円の中心と半径はどうなるであろう.原像の円の直径をP(z1),Q(z2)(原点に近いほうをP)とする.原点からの距離はPが最も小さく,Qが最も大きい.P,Qの像をP'(z1),Q'(z2)とすると,変換された円はP'Q'を直径とする円である(今度は原点に近いほうがQ').ここで,
P'Q'=|1/z1−1/z2|=|(z1-z2)/z1z2|=PQ/ OP・OQ
より,変換された円の直径はもとの円の直径を,OP・OQで割った値となる.また,
(z1+z2)/2=(1/ z1+1/ z2)/2=(z1+z2)/2z1z2=1/z1z2 ・(z1+z2)/2
より,変換された円の中心はもとの円の中心をz1z2で割ったものとなる.ここでz1z2とは有向線分OP,OQの積を考えることで,もとの円が原点を含む場合にも対応できる.
 |
 |
具体例で見てみる.
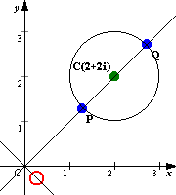
(1)中心C(2+2i),半径1の円の変換
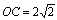 より, より,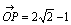 , ,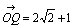 ∴ 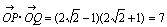 ∴ 変換された円の 中心は C'(2/7-2i/7),半径は1/7 |
 |
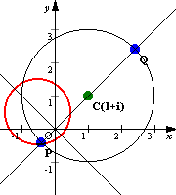
(2)中心C(1+i),半径2の円
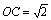 より, より,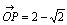 , ,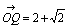 ∴ 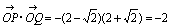 ∴ 変換された円の 中心は C'(−1/2+i/2),半径は2×1/2=1 |
 |