《Ｏｎｅ Ｐｏｉｎｔ》 変数は関数の種類により固定されている． 　陽関数：x，　陰関数：x,y 　，媒介変数：t　　，極形式：t　 　パラメータとしては変数欄右にある a,b,c,d の４つが使用可能である． [ｸﾞﾗﾌ表示]→[ﾊﾟﾗﾒﾀ表示]を選ぶ．ﾊﾟﾗﾒｰﾀｰの増減幅を設定してから[描画]をｸﾘｯｸする．ｸﾘｯｸするたびにｸﾞﾗﾌが描画されていく．

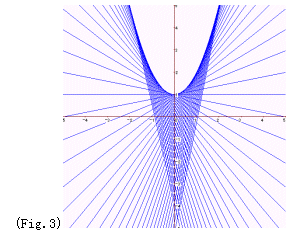
課題５　a があらゆる実数値をとりながら変化するとき，直線 y=：2ax-a^2+1 の通りうる範囲を図示せよ． 　※包絡線の図形を楽しみたいものです．(Fig.3)

課題６　次の関数において,ﾊﾟﾗﾒｰﾀｰを変化させてｸﾞﾗﾌの変化を考察しなさい．

�@ 極形式による２次曲線の分類

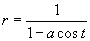　⇔ r=：1/(1-acos(t)) ( 0<t<8)

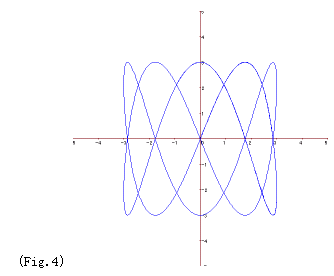
�A ﾘｻｰｼﾞｭ曲線

　x=：3sin(at) , y=：3sin(bt) ( 0<t<8)

＊増減幅を１と設定しa，bの片方ずつ，または両方を同時に変化させてみよう．

　a=2,b=5 のときは 右図(Fig.4)

課題７　放物線 y=：x^2-2ax+2a+3 は定点を通る．残像を残して描画しその定点を確認せよ．

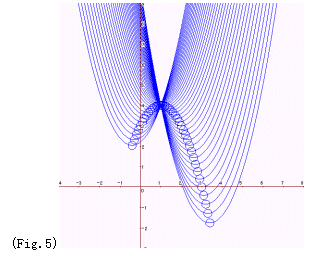※右図(Fig.5)は，描画領域の変更をした後，残像を残し，ﾊﾟﾗﾒｰﾀｰを変化させ描画している．
描画した後，領域を変更すると以前に描いたｸﾞﾗﾌは消去されて最後のｸﾞﾗﾌだけが残る．
尚，残像が上手くいかないときは残像のON⇔OFFをしてみると動作するようになる．

課題８　課題７の放物線の頂点も同時に描画してその軌跡を考察せよ．

※課題４ のﾋﾝﾄを参照してﾊﾟﾗﾒｰﾀｰを埋め込め(Fig.5)