(1)最大最小問題のシミュレーション
①区間を変化させる
| ex.5) y=-x2+2x+1 の a≦x≦a+1 における最大値・最小値 |
手順1:[関数入力] 陽関数 y=:-x^2+2x+1]⇒[グラフ表示] 標準表示
手順2:[区間の設定・解除] 区間設定
区間の下限:0 ,区間の上限:2
※下限・上限の値は後から変更可能
※ここで,区間が黄色網掛けで表示される
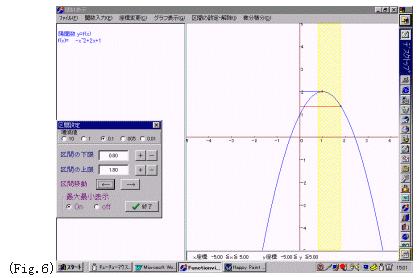
手順3:増減値(通常は0.1)を指定し,区間移動の矢印をクリックして区間を移動させる.
手順4:[最大最小表示]のON,OFFにより最大値・最小値の位置が表示される.(Fig.6)
| 課題9 (ex.5)において,区間を 0≦x≦a とするときの最大値・最小値を考察せよ. |
②関数を変化させる
| ex.6) 2次関数 y=x2-2ax+2a-1 の区間 0≦x≦2 における最大値・最小値 |
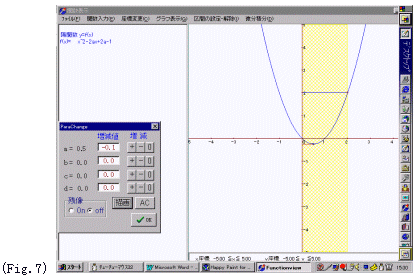
手順1:[関数入力] 陽関数 y=:x^2-2ax+2a-1
手順2:[区間の設定・解除] 区間設定
区間の下限:0 ,区間の上限:2
最大最小表示 ON (注)OFFをクリックしてから再度ONをクリックすると確実
※ここで,区間が黄色網掛けで表示される
[終了]
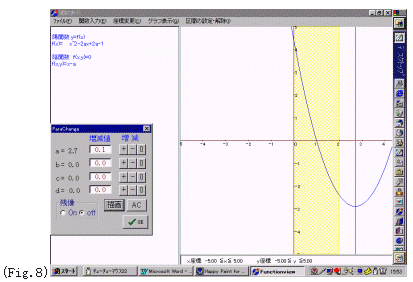
手順3:[グラフ表示] パラメタ表示
パラメーター aの増減値を指定し描画してシミュレーションする
| 課題10 (ex.5)において,放物線と軸が同時に移動するように改良せよ. |
※この場合は,最大値・最小値の位置は表示不能となるようである.
ここでは,区間の端と軸との位置関係を確認することを目的とする.