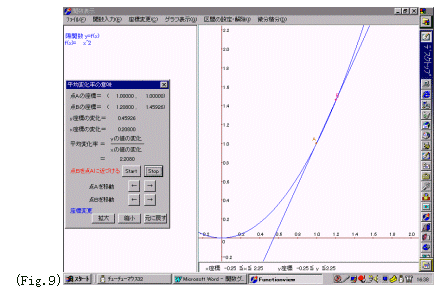
ex.7) f(x)=x2において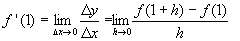 の図形的意味を考察する. の図形的意味を考察する.
|
手順1:[関数入力] 陽関数 y=:x^2]⇒[グラフ表示] 標準表示
手順2:[微分積分] 平均変化率
点Aのx座標:1 ,点Bのx座標:2
※これらの値は後から変更可能
※ここで,割線ABが描画され,ダイアログボックスが表示される.
手順3:[点Bを点Aに近づける]Start
※割線が点Aにおける接線に近づく様子が描画される.
①続けて[拡大]をクリックしてみよう.
手順4:[Stop]をクリックすると,Bは止まる.
※描画中に,点A,Bを移動することも可能である.
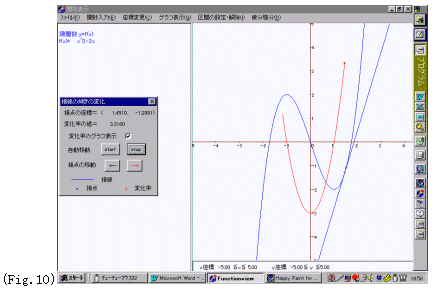
(3)接線の変化をシミュレーション〜陽関数のみ可能
| ex.8)関数f(x)=x3-3xにおいて、導関数f'(x)を接線の傾きの値からシミュレートする. |
手順1:[関数入力] 陽関数 y=:x^3-3x]⇒[グラフ表示] 標準表示
手順2:[微分積分] 接線の変化
※この時点で,ある接点での接線が描画され,その傾きの値が赤点で描画される.
手順3:[自動移動]Start,Stop をクリックし接点を移動する.
※[接点の移動]→,←をクリックすることで移動の向きを変えられる.
手順4:[変化率のグラフ表示]をチェックすることで接線の傾きの値の軌跡が描画できる.
これにより,f(x)=x3-3xの導関数f'(x)=3x2-3の変化を視覚化できる.
※上記の操作は,接点の移動中に変更可能である.
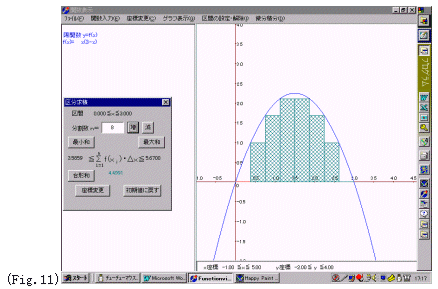
(4)区分求積のシミュレーション
ex.9)放物線y=x(3-x)とx軸で囲まれる図形の面積が 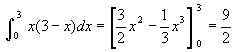 となることを、区分求積法で確認しよう. となることを、区分求積法で確認しよう.
|
手順1:[関数入力]陽関数 y=:x(3-x)]⇒[グラフ表示] 標準表示
※描画領域を変更して見易い位置にする.
手順2:[微分積分] 区分求積
区間の下限:0 ,区間の上限:3
※この時点で,区分求積のダイアログボックスが表示される.
手順3:‘最大和’,‘最小和’のどちらかをクリックする.
手順4:[分割数]を(増),(減)で変化させるとグラフが描かれ
計算値がダイアログボックスに次々と表示される.