(Fig.4-1)
(Fig.4-2)
(Fig.4-3)
(Fig.4-4)
(Fig.4-5)
(Fig.4-6)
| (4)関数の最大値・最小値(定義域が変化) GRAPES ,FunctionView |
関数f(x)=(3-x)|x+1|のt≦x≦t+1におけるf(x)の最小値をg(t)とする．
(1)y=f(x)のグラフを描け．
(2)y=g(t)のグラフを描け．
(3)-2≦t≦3におけるg(t)の最大値・最小値を求めよ。この問題は，私が今年担当している３年生の問題演習のときに行ったものである．
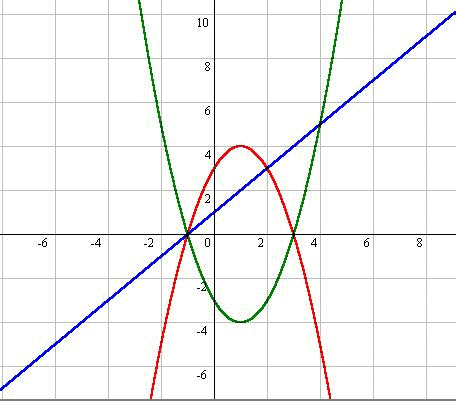
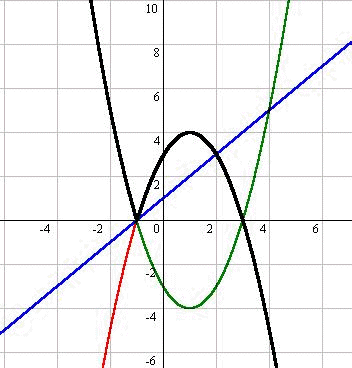
- では，f(x)の場合分けの明示のため，f(x)=(3-x)(x+1)，f(x)=-(3-x)(x+1)，f(x)=x+1の３つのグラフを併記している．グラフ描画の際のの場合分けの境界が理解でき，y=f(x)のx切片がx=3,−1であることが理解できればＯＫとなる．(Fig.4-1, Fig4-2)
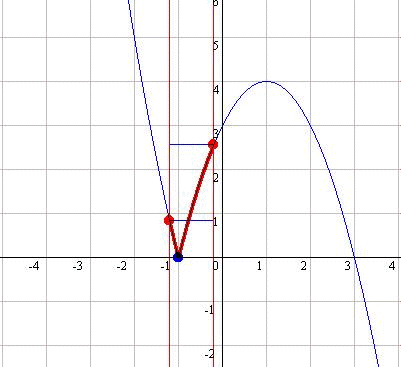
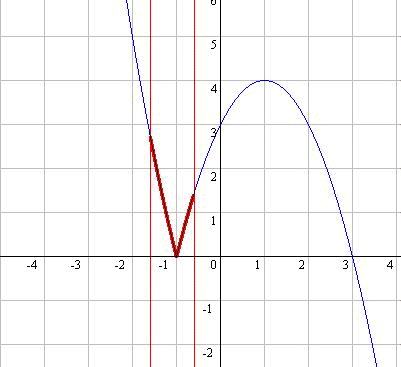
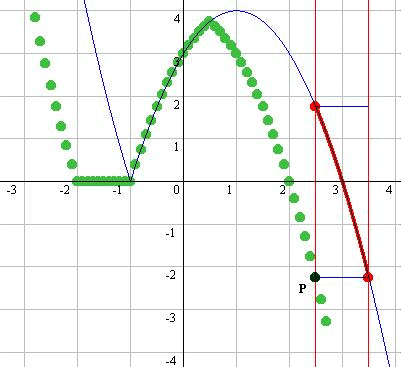
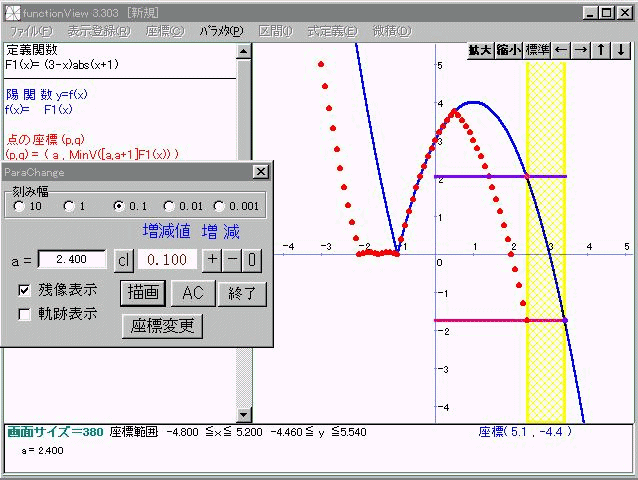
- ﾊﾟﾗﾒｰﾀtの変化に伴って変化する定義域を赤で明示する(Figt.4-3, 4-4)．FunctionViewでは予め区間の設定が用意されており定義域を黄色斜線で明示するなど簡単に設定でき，MAX,MINの表示も可能である(Fig4-6)．あとは，最小値の点をx=t上に残像を残してy=g(t)の概形を眺めてみよう(Fig.4-5)．
(Fig.4-1)
(Fig.4-2)
(Fig.4-3)
(Fig.4-4)
(Fig.4-5)
(Fig.4-6)