数　学　Ⅱ　　《積　分》　Ｎｏ．２　　区分求積法

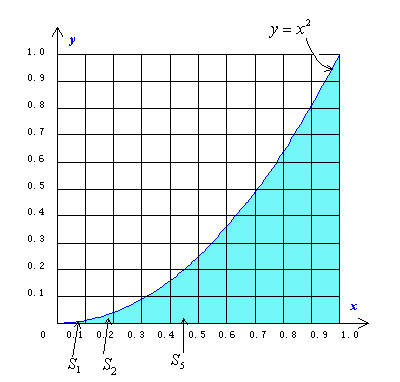　右のような曲線に囲まれた面積を求める方法として、よく用いられたのが区分求積法でした。図のように、いくつもの長方形に分け、ひとつひとつの面積を計算し、最後にそれらを合計するという点でこれはまさに積分（細かく分けて、かけて、たす）です。

【１】右の面積を区分求積法で求めよう。

長方形の面積＝　（たて）　×　（よこ）
　　　S1　　＝　　(0.1)2　×　(0.1)　　＝　0.001
　　　S2　　＝　　(0.2)2　×　(0.1)　　＝　0.004
　　　S3　　＝　　(0.3)2　×　(0.1)　　＝　0.009
　　　S4　　＝　　(0.4)2　×　(0.1)　　＝　0.016
　　　S5　　＝　　(0.5)2　×　(0.1)　　＝　0.025
　　　S6　　＝　　(0.6)2　×　(0.1)　　＝　0.036
　　　S7　　＝　　(0.7)2　×　(0.1)　　＝　0.049
　　　S8　　＝　　(0.8)2　×　(0.1)　　＝　0.064
　　　S9　　＝　　(0.9)2　×　(0.1)　　＝　0.081
　＋）S10　 ＝　　(1)2　　×　(0.1)　　＝　0.1 　　　　　

　　　S　　＝　　0.385




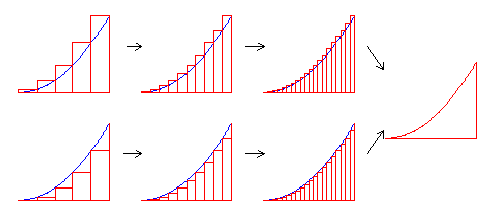
【２】誤差をもっとなくすには、どうしたらよいか？

　　もっと細かく分ければよい！




【３】［資料２］から最終的にこの面積はいくつになるか？

　　0.333･･･＝1/3




［資料１］区分求積法の理論

［資料２］パソコンによる計算値

10 == 0.385000   41 == 0.345628   80 == 0.339609   290 == 0.335059   930 == 0.333871
11 == 0.380165   42 == 0.345333   81 == 0.339532   300 == 0.335002   940 == 0.333865
12 == 0.376157   43 == 0.345051   82 == 0.339456   310 == 0.334948   950 == 0.333860
13 == 0.372781   44 == 0.344783   83 == 0.339382   320 == 0.334897   960 == 0.333854
14 == 0.369898   45 == 0.344527   84 == 0.339309   330 == 0.334850   970 == 0.333849
15 == 0.367407   46 == 0.344282   85 == 0.339239   340 == 0.334805   980 == 0.333844
16 == 0.365234   47 == 0.344047   86 == 0.339170   350 == 0.334763   990 == 0.333839
17 == 0.363322   48 == 0.343822   87 == 0.339102   360 == 0.334724   1000 == 0.333834
18 == 0.361626   49 == 0.343607   88 == 0.339037   370 == 0.334686   1100 == 0.333788
19 == 0.360111   50 == 0.343400   89 == 0.338972   380 == 0.334650   1200 == 0.333750
20 == 0.358750   51 == 0.343201   90 == 0.338909   390 == 0.334616   1300 == 0.333718
21 == 0.357521   52 == 0.343010   91 == 0.338848   400 == 0.334584   1400 == 0.333691
22 == 0.356405   53 == 0.342827   92 == 0.338788   410 == 0.334554   1500 == 0.333667
23 == 0.355388   54 == 0.342650   93 == 0.338729   420 == 0.334525     ・・・  
24 == 0.354456   55 == 0.342479   94 == 0.338671   430 == 0.334497        
25 == 0.353600   56 == 0.342315   95 == 0.338615   440 == 0.334471        
26 == 0.352811   57 == 0.342157   96 == 0.338560   450 == 0.334445        
27 == 0.352080   58 == 0.342004   97 == 0.338506   460 == 0.334421        
28 == 0.351403   59 == 0.341856   98 == 0.338453   470 == 0.334398   8600 == 0.333391
29 == 0.350773   60 == 0.341713   99 == 0.338401   480 == 0.334376   8700 == 0.333391
30 == 0.350185   61 == 0.341575   100 == 0.338350   490 == 0.334354   8800 == 0.333390
31 == 0.349636   62 == 0.341441   110 == 0.337893   500 == 0.334334   8900 == 0.333390
32 == 0.349121   63 == 0.341312   120 == 0.337512   510 == 0.334314   9000 == 0.333389
33 == 0.348638   64 == 0.341187   130 == 0.337189   520 == 0.334295   9100 == 0.333388
34 == 0.348183   65 == 0.341065   140 == 0.336913   530 == 0.334277   9200 == 0.333388
35 == 0.347755   66 == 0.340947   150 == 0.336674   540 == 0.334260   9300 == 0.333387
36 == 0.347351   67 == 0.340833   160 == 0.336465   550 == 0.334243   9400 == 0.333387
37 == 0.346969   68 == 0.340722   170 == 0.336280   560 == 0.334227   9500 == 0.333386
38 == 0.346607   69 == 0.340615   180 == 0.336116   570 == 0.334211   9600 == 0.333385
39 == 0.346263   70 == 0.340510   190 == 0.335970   580 == 0.334196   9700 == 0.333385
40 == 0.345938   71 == 0.340409   200 == 0.335838   590 == 0.334181   9800 == 0.333384
        72 == 0.340310   210 == 0.335718           9900 == 0.333384
        73 == 0.340214   220 == 0.335610           10000 == 0.333383
        74 == 0.340121   230 == 0.335510                
        75 == 0.340030   240 == 0.335420                
        76 == 0.339941   250 == 0.335336                
        77 == 0.339855   260 == 0.335259                
        78 == 0.339771   270 == 0.335187                
        79 == 0.339689   280 == 0.335121