数　学　�U　　《積　分》　Ｎｏ．３　　ニュートンの発見

　鉄腕アトムがx秒間に進む距離を求めてみよう。

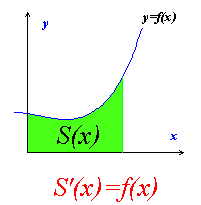
　微分の創始者ニュートンはS(x)と曲線y=x²の間に、ある関係を発見しました。どんな関係だったのでしょう？

S'(x)=(x³/3)'=(x³)'/3=3x²/3=x²
面積の式S(x)を微分すると曲線の式になる!!（距離を求めると速さになる）

曲線に囲まれた面積を求めることは古代エジプト時代からの課題でした。長い間、区分求積法のような積分（細かく分けて、かけて、たす）が使われていましたが、現代のようにコンピュータがあるわけでもなく、その計算は非常に面倒なものでした。 　ところが、17世紀になり運命的な出会いがやってきました。イギリスの数学者ニュートンによって微分が誕生すると、それまで無関係に思われていた微分と積分が互いに逆演算というわかりやすい形で結ばれ（微積分学の基本定理）、面倒だった積分の計算がとても簡単に、しかも早くできるようになりました。積分にしてみれば、微分さまさまといったところでしょう。 　 　　微分・積分・いい気分！

　

　「微積分学の基本定理」からアトムの問題を解いてみましょう。

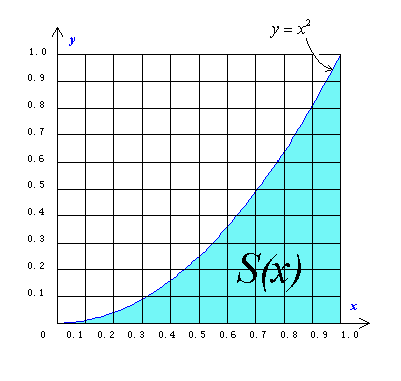　「微積分学の基本定理」から

　　　　S'(x)=x²
よって
　　　　S(x)=x³/3
　　　∴　S(1)=1/3
　　　　　S(2)=8/3
　　　　　S(3)=27/3