「はい、こちら２次不等式探検班ですっ。」油を売っていた隊長に待望の捜査命令の電話が響いた。

　研究班では、の交点を見つけるには「」を用いれば判断できるとレーダーでキャッチした。隊長は老いているため若い隊員４人を現地に飛ばした。

　ところで、気になる捜査命令の内容は「の場合、どのような解の種類があるか」というものである。他のの解についての捜査はもうすでに解明済みであるという。

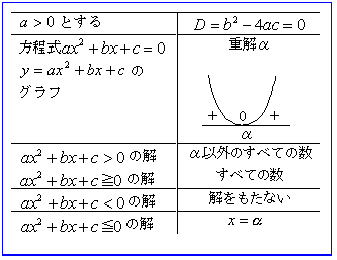　隊員たちは、ヘリから降り目の前にした４つの洞窟に心が凍った。こういう場合、一人一つの洞窟に入らなければいけないからだ。隊員１は、 と書いてある道に進んだ。隊員２は、 へ、隊員３は へ、隊員４は へと進んだ。

　隊員４は、無線でみんなに問いかけた。

　「オイ。このグラフの形をした床に“α”文字がどのくらいあるかを調査しろってことだろ？」

　他の隊員は、不安そうに

　「そうなんじゃない？」

と答える。

　しばらくの間は、みんな“α”文字を探しているのだろうか無線は途絶えたままだった。１時間後、４人ともヘリに戻ってきた。

　隊員２「俺の入ったの洞窟はグラフの床に一つも“α”文字がなかったぞ。」と、それぞれ語り始めた。隊員１は「私の所は、やたらと“α”以外の文字がたくさんあって“α”文字なんか一つもなかったわ。」隊員４は「ぼくの所は、あの広いグラフの床を探しても一つしかなかったぜー。」隊員３は「私の所は、ありとあらゆる実数の最先端に“α”文字が一つあったわ。」などと語っているうちにヘリが事務所に着いた。

　隊員たちは、調査内容を詳しく研究班に伝えた。おかげでの謎が解けた。今回の調査結果を基にしてコンピュータで分析すると、の場合の解も解明できた。

　この立派な活躍ぶりは、教科書にきちんと載って生徒たちが勉学に励んでいるそうです。隊員たちの熱い闘いは、それ以後現れることはなかった。　　　　　　　−おわり−