この章の最初で、微分と積分の役割について、 微分：接線の傾きの値を計算して、曲線の各点で接線を引いて、その点での状況を調べる。 積分：曲線で囲まれた面積を計算する。 と説明しました。さて、積分の役割の面積計算ですが、どんな面積も、長方形の面積のように、 「たて×横」 のような簡単な計算で求められるのであれば、なにも「積分」などともっともらしいものを考える必要もありませんでした。

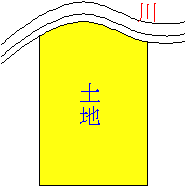　しかし、曲線に囲まれた面積を求めることは古代エジプト時代からの課題でした。たとえば、ナイル川はすぐに氾濫しますし、その削り取られた土地は大体において変形な曲線の図形になることが多いのです。みんなは右図のような面積をどのように計 算しますか。

　ギリシア人アルキメデスは、その土地を細かく分けて計算し、その和を求めました。かれはこの方法で円周率πの値も求めたのです。
　　［アルキメデスの円周率：プリントの裏にあります］

　つまり、「積分」とは、 細かく分けて、かけて、たす ということであり、「かけ算を発展させたもの」と考えたらとても簡単です。そこで、積分を考えるスタートとして、たて×横で面積を求めることができない図形の面積を考えてみよう。

　
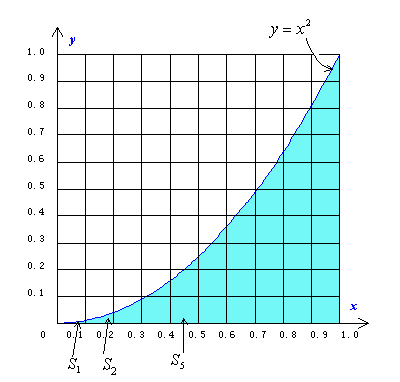問題１:右図のような曲線に囲まれた面積Ｓ(曲線y=x²，ｘ軸，直線x=1に囲まれた面積)を求める方法としてよく用いられたのが、区分求積法でした。
　図のようにいくつもの長方形に分け、一つ一つの面積を計算し、最後にそれらを合計するという点で、これは、まさに積分(細かく分けて、かけて、たす)です。

(1)右上の面積を区分求積法で求めてみよう。

長方形の面積＝　（たて）　×　（よこ）
　　　S₁　　＝　　(0.1)²　×　(0.1)　　＝　0.001
　　　S₂　　＝　　(0.2)²　×　(0.2)　　＝　0.004
　　　S₃　　＝　　(0.3)²　×　(0.1)　　＝　0.009
　　　S₄　　＝　　(0.4)²　×　(0.1)　　＝　0.016
　　　S₅　　＝　　(0.5)²　×　(0.1)　　＝　0.025
　　　S₆　　＝　　(0.6)²　×　(0.1)　　＝　0.036
　　　S₇　　＝　　(0.7)²　×　(0.1)　　＝　0.049
　　　S₈　　＝　　(0.8)²　×　(0.1)　　＝　0.064
　　　S₉　　＝　　(0.9)²　×　(0.1)　　＝　0.081
　＋）S₁₀　 ＝　　(1)²　　×　(0.1)　　＝　0.1 　　　　　

(2)(1)で求めた面積を、実際の面積Ｓに近づけるためには　どのようにしたらよいか

　　　　答え　細かく分ける、あまっているところを引く、さかさまにくっつける

(3)下記の資料から最終的にこの面積はいくらになると考えられるか。

　　　　答え　0.3、0.333･･･ など　→　1/3

［資料１］−区分求積法の理論−

［資料２］−パソコンによる計算値−

　
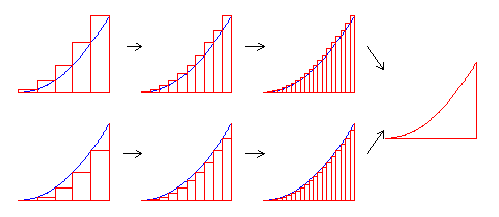
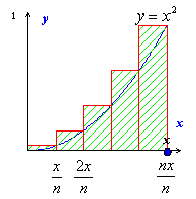問題２:右図の斜線部分の面積Ｓ_ｎを求めなさい。
　そして、長方形の数をどんどん増やしていき、Ｓ(x)を求めなさい。
[準備]

　1)　

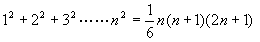
　2)　

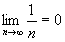
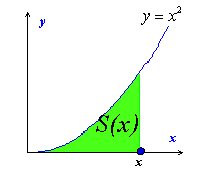[解]右上の図において、左から１番目の長方形は

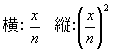
です。　同じように考えて、ｎ番目の長方形は

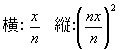
ですから、ｎ個の長方形の面積の総和Ｓｎは次の式で表されます。

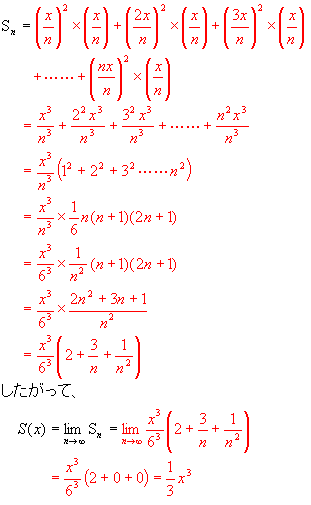
＜説明＞問題１のSは、問題2で言えばS(1)のことである。
　　S(x)＝x³/3において
　　　　　S(1)=1³/3=1/3
　問題１の結果と比較して、S(x)=x³/3が正しいことがわかる。

【プリント2】　【プリント3】　【プリント4】