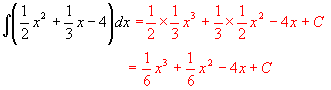
前のプリントの問題６で

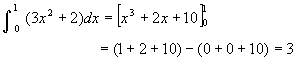
は、正しいと思いましたか、それとも間違いだと思いましたか？　問題５で解いたときと比べると、［　］の中に+10 があり、

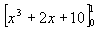
となっていますが、答えは問題５で解いたときと同じ 3 です。また、-1 や +5 を付けてみても

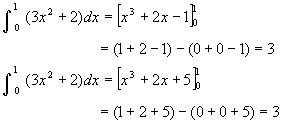
と、どれも同じ答えになります。さらに、Ｃをある定数として付けてみても、

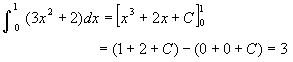
と、やはり同じです。すなわち、

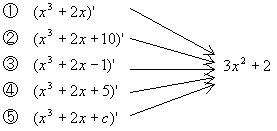
となりますから、�@から�Dのどれを使って定積分しても同じ結果になるのは当然と言えば当然です。それならば、１番楽な�@で定積分するのがベストですよね！

　しかし、微分したら3x²+2になる関数は？ と問われたら�@〜�Cはすべて正しく、さらに、�@〜�C以外にも微分したら3x²+2になる関数は無数にあります。前のプリントで登場したライプニッツは、この、「微分したら3x²+2になる関数」を、

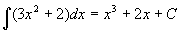
と表しました。ここで、「Ｃ」は定数を表しています。（Ｃを”積分定数”と言います。）

　このような積分を不定積分と言います。

　時代の流れから見ると、定積分はグラフの面積を求めようとして誕生したのに対し、不定積分はグラフの接線を求めようとして生まれた微分法の逆演算として起こったもので、もともと源流が違うのです。このように、積分には二つの積分があるのです。

例１　次の不定積分を計算せよ。

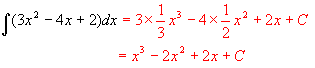
問題７:次の不定積分を計算せよ。

(1)

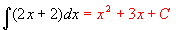
(2)

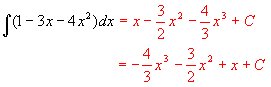
(3)

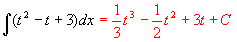
(4)

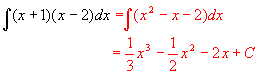
(5)

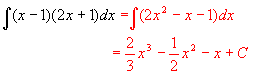
(6)

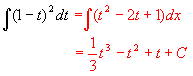
(7)

【プリント1】　【プリント2】　【プリント3】