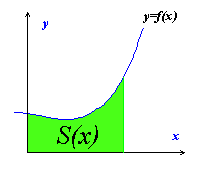
前回のプリントで分かったとおり、このように区分求積法の理屈はさほど難しいものではなく、古代から発見されていたのですが、いかんせん、実際の計算が大変でした。それで、なかなか積分は発展しなかったのです。このプリントの裏を参照して下さい。
 しかし、微分の創始者ニュートンは面積S(x)と曲線の方程式の間に、ある関係を発見しました。この運命的な発見が、その後の積分をより簡単なものとし、発展させたのです。その発見をみんなも体験してみよう!
しかし、微分の創始者ニュートンは面積S(x)と曲線の方程式の間に、ある関係を発見しました。この運命的な発見が、その後の積分をより簡単なものとし、発展させたのです。その発見をみんなも体験してみよう!
斜線部分の面積をS(x)とします。次の関数についてS(x)を計算してみましょう。
①y=1(定数関数)----------------
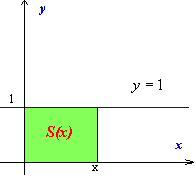 S(x)=1×x
S(x)=1×x
このとき、関数:f(x)=1
面積:S(x)=x
②y=x(1次関数)----------------
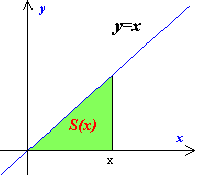 S(x)=1/2×x×x
S(x)=1/2×x×x
このとき、関数:f(x)=x
面積:S(x)=x2/2
③y=x+1(1次関数)--------------
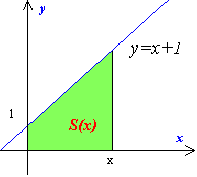 S(x)=1/2×{(x+1)+1}×x
S(x)=1/2×{(x+1)+1}×x
=x(x+2)/2=x2/2/2+x
このとき、関数:f(x)=x+1
面積:S(x)=x2/2+x
④y=x2 (2次関数)--------------
前回のプリント「積分1」より S(x)=x3/3 である。
このとき、関数:f(x)= x2
面積:S(x)=x3/3
以上①~④で関数f(x)と面積S(x)をようく見てみると、何か気がつきませんか
微分の創始者ニュートンは、関数f(x)と面積S(x)の間にある関係を最初に発見しました。さて、どんな関係だったのでしょう。下の空欄に書いてみて下さい。
面積S(x)を微分すると、関数f(x)になる。*生徒から答えが出ないときは、例を示し( )を発問する。
例 ・f(x)=3のとき、S(x)=3x → ・f(x)=3x2のとき、S(x)=( )
・f(x)=2xのとき、S(x)=x2 → ・f(x)=4xのとき、S(x)=( )
17世紀、イギリスの数学者ニュートンによって微分が誕生しました。そして、そのニュートンによるこの運命的な発見により、それまで無関係と思われていた微分と積分が互いに逆演算というわかりやすい関係で結ばれ、面倒だった積分の計算がとても簡単に、しかも早くできるようになったのです。積分にしてみれば、微分サマサマといったところでしょう。
|
|
問題3:微分積分学の基本定理を使って、次の面積をラクラク積分してみなさい。
(1)
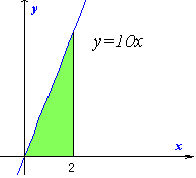 基本定理より
基本定理より
S'(x)=10x
よって
S(x)=5x2
S(2)=5×22=20
(2)
よって
S(x)=x2/2+5x
S(10)=102/2+5×10=100
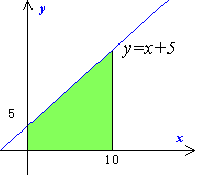 S'(x)=x+5
S'(x)=x+5
(3)
よって
S(x)=x3
S(2)=23=8
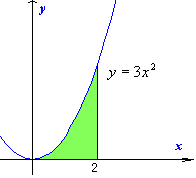 S'(x)=3x2
S'(x)=3x2
問題4:ちょっと一工夫して、次の面積をラクラク積分してみなさい。
(1)
よって
S(x)=x3/3
S=S(2)-S(1)
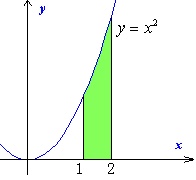 S'(x)=x2
S'(x)=x2
=23/3-13/3=7/3
(2)
よって
S(x)=x3/3-x2+2x
S=S(4)-S(2)
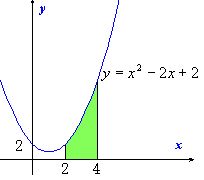 S'(x)=x2-2x+2
S'(x)=x2-2x+2
=(43/3-42+2×4)-(23/3-22+2×2)
=64/3-16+8-8/3+4-4=32/3