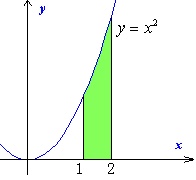
ラクラク積分では、次のように面積を計算しました。
基本定理からＳ'(x)＝x2 よって S(x)=x3/3
S=S(2)−S(1) |
この計算を、記号づくりの名人と言われたドイツの数学者ライプニッツは次のように書きました。
 |
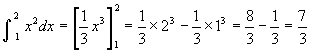記号はインテグラルといい、「たす」と言う意味のドイツ語「Summation」の頭文字Ｓを縦に引き伸ばしたものです。
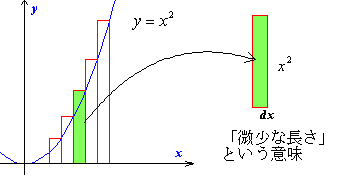もともと積分とは区分求積法に見られるように、いくつもの長方形に分け、ひとつひとつの面積を計算し、最後にそれらを合計する(細かく分けて、かけて、たす)ことでした。ライプニッツは図のように細かく分けた長方形のうち、あるひとつの長方形の面積を
x2dx
と表し、長方形を端から端(1から2まで)までたすことをインテグラルで表しました。
このように、積分の記号には「細かく分けて、かけて、たす」という積分の歴史的，本質的な意味合いが込められているのです。
面積を計算するときには、どこからどこまでの面積なのか、範囲がはっきり定まっていなければなりません。
そこでこのような積分を定積分と言います。
|
|
積分の計算をするときは、右のことを覚えておくと便利です。
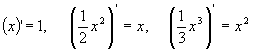
問題５:ライプニッツの記号で表された、次の計算をしなさい。
(1)
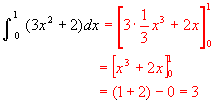
(2)
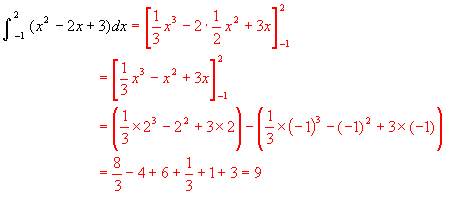
(3)
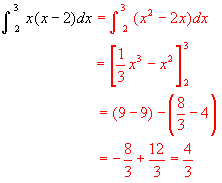
(4)
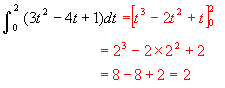
問題６:次の計算は正しいでしょうか。？
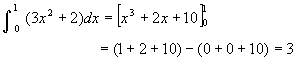
2年1組では 正しい･･･13人 まちがい･･･25人
