| 14 本時の目標 |
|
| 15 本時の内容 |
| ねらい | 学 習 活 動 →:指示・説明[教師],⇒発問・活動[生徒] |
指導上の留意点および評価 (○:留意点,□評価) |
||||||||
| 導入 前時の復習 (5分) |
→コンピュータを起動し,GRAPESを立ち上げなさい。 ⇒コンピュータを起動し,GRAPESを呼び出す。 →(p.100 問11)r=a/(1-cosθ)をGRAPESに入力させる。 ⇒入力し,放物線であることを確認する。 |
○極方程式は基本図形で入力することを注意する。また,パラメータθの値は0から2π(≒6.3)まで変化させる。 (□関心・意欲・態度) 指示どおり意欲的に取り組んでいるか。 |
||||||||
| 展開1 二次曲線の極方程式 (15分) |
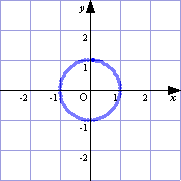
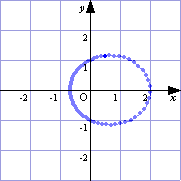
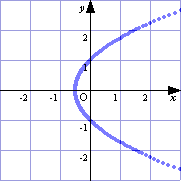
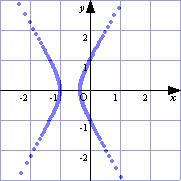
→学習フロッピーを配布し,極方程式r=a/(1-bcosθ)…①を入力させる。 ⇒①を入力する。 →a,bの値を変化させて,グラフのようすを観察させる。 ⇒GRAPESのパラメータa,bの値を変えて入力し,いくつかのグラフのパターンを学習フロッピーの学習プリントに貼り付ける。 →b=1のときは放物線だが,他の値でも放物線になることはあるだろうか。 【例】
|
(□関心・意欲・態度) 課題の内容を理解しようという態度を示しているか。 ○a,bのうち一方を固定して,パラメータを変化させる。 (□表現・処理) a,bの変化がグラフにおいてどのような意味を持つか理解できるか。 ○机間指導して生徒の支援をする。 (□数学的な考え方) |b|<1で楕円(b=0で円),|b|=1で放物線,|b|>1で双曲線と予想できるか。また,aの値は,グラフを極中心にa倍に拡大することに気がつくか。 ○実際にGRAPESの基本図形に入力し,例えば(a,b)=(1,2)でθを0から2π(≒6.3)まで変化させると,漸近線も一緒に描かれる。(下図) 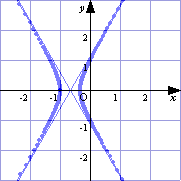 |
||||||||
|
展開2 直交座標に直す。 (15分) |
→①の分母を払って,r-brcosθ=a 移行すると,r=brcosθ+a これに,r=√(x2+y2),rcosθ=xを代入し,両辺を平方し移項すると, (1-b2)x2+y2-2abx-a2=0 …② これを,GRAPESに入力させる。 ⇒②をGRAPESに入力し,パラメーターa,bの値を変え,いくつかのグラフのパターンを学習フロッピーの学習プリントに貼り付ける。 →x2の係数から,|b|<1,|b|=1,|b|>1に場合分けできることを確認。 |
画面を一斉送信して,説明に集中できるようにする。 ○GRAPESに入力するときは陰関数で。 (□知識・理解) ①と②が一致することが確認できたか。 |
||||||||
| 本時のまとめ (15分) |
→(まとめ)極方程式r=a/(1-bcosθ)は,二次曲線を表す。|b|<1のとき楕円(b=0で円),|b|=1のとき放物線,|b|>1のとき双曲線を表す。 ⇒学習プリントを印刷し,提出する。 →次時は,レポート課題4の続きをやることを予告する。 ⇒パソコンを手順に従って終了させる。 |
(□知識・理解) コンピュータを使うことで,図形の問題を具体的に見ながら考えていくことが有効であること。また,予想したことが計算によって確かめられることから,計算の必要性について理解されたか。 |