(1) k=-2,0,2偺偲偒丆僌儔僼C傪恾帵偣傛丅
(2) (1)偺俁偮偺僌儔僼偼丆嫟捠側侾揰傪捠傞丅偦偺揰偺嵗昗傪媮傔傛丅
(1) k=-1,0,1偺偲偒丆偙偺娭悢偺僌儔僼傪偐偗丅
(2) (1)偺娭悢偺僌儔僼偲x幉偲偺嫟桳揰偺屄悢傪丆偦傟偧傟媮傔傛丅
(1) y=x3-4x+1,-3亝x亝3,-10亝y亝10
(2) y=-x4+4x2,-3亝x亝3,-10亝y亝5
(1)
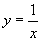 丂 丂丂(2)
丂 丂丂(2) 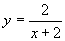
(1)
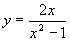 丂丂丂(2)
丂丂丂(2) 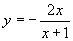
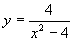 偼丆
偼丆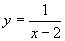 偲
偲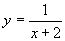 偺嵎偲側偭偰偄傞丅偙偺俁偮偺僌儔僼傪偐偄偰丆偦偺傛偆偡傪妋偐傔傛丅
偺嵎偲側偭偰偄傞丅偙偺俁偮偺僌儔僼傪偐偄偰丆偦偺傛偆偡傪妋偐傔傛丅
(1) y=sin x,-4亝x亝10,-2亝y亝2丂丂丂(2) y=sin x+cos 2x,-4亝x亝10,-2亝y亝2
(1)
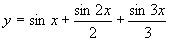 ,-4亝x亝10,-2亝y亝2
,-4亝x亝10,-2亝y亝2(2)
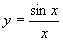 ,x亗0,-10亝x亝10,-1亝y亝2
,x亗0,-10亝x亝10,-1亝y亝2
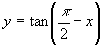 ,-4亝x亝4偺僌儔僼傪偐偗丅
,-4亝x亝4偺僌儔僼傪偐偗丅
(1) y=ex丂丂丂(2) y=ex-e-x
(1) y=x-log x丂丂丂(2) y=x log x
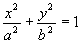 偱a,b偺抣偑曄壔偡傞偲僌儔僼偼偳偆側傞偐丅
偱a,b偺抣偑曄壔偡傞偲僌儔僼偼偳偆側傞偐丅
(1)
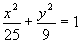
(2)
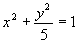
(3) 3x2+2y2=6
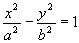 乧嘆偲
乧嘆偲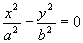 乧嘇偵偮偄偰丆師偺栤偄偵摎偊傛丅
乧嘇偵偮偄偰丆師偺栤偄偵摎偊傛丅(1) 嘇偼嘆偺壗偐丅
(2) 傑偨丆a,b偑曄壔偡傞偲嘆偺僌儔僼偼偳偆側傞偐丅
(1)丂 y=-2x2丂丂丂 (2) x2-2y=0
(1) y2=4x丂丂丂(2) x+8y2=0
(1) y=2x2-1丂丂丂(2) y=x2+x+1
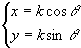 傪GRAPES偺婎杮恾宍偵擖椡乮巆憸丒婳愓僠僃僢僋乯偟偰丆僷儔儊乕僞兤傪曄壔偝偣偰傒傛丅偳偺傛偆側婳愓傪昤偔偐丅傑偨丆k傪曄壔偝偣傞偙偲偵傛偭偰丆k偼偦偺婳愓偺壗傪昞偟偰偄傞偐丅嵟屻偵丆k=2偺偲偒偺僌儔僼傪揧晅偣傛丅
傪GRAPES偺婎杮恾宍偵擖椡乮巆憸丒婳愓僠僃僢僋乯偟偰丆僷儔儊乕僞兤傪曄壔偝偣偰傒傛丅偳偺傛偆側婳愓傪昤偔偐丅傑偨丆k傪曄壔偝偣傞偙偲偵傛偭偰丆k偼偦偺婳愓偺壗傪昞偟偰偄傞偐丅嵟屻偵丆k=2偺偲偒偺僌儔僼傪揧晅偣傛丅
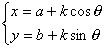 偼偳偺傛偆側恾宍傪昞偡偐丅嶲峫恾傕揧晅偣傛丅
偼偳偺傛偆側恾宍傪昞偡偐丅嶲峫恾傕揧晅偣傛丅
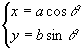 偼偳偺傛偆側恾宍傪昞偡偐丅a亗b偺嶲峫恾傕揧晅偣傛丅
偼偳偺傛偆側恾宍傪昞偡偐丅a亗b偺嶲峫恾傕揧晅偣傛丅
(1)
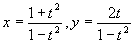 丂丂丂(2)
丂丂丂(2) 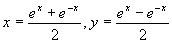
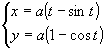 偺僌儔僼傪偐偗丅
偺僌儔僼傪偐偗丅
丂丂丂
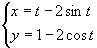 (-15亝t亝15)
(-15亝t亝15)
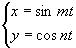 (0亝t亝2兾)傪揧晅偣傛丅
(0亝t亝2兾)傪揧晅偣傛丅
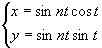 (0亝t亝2兾)傪揧晅偣傛丅
(0亝t亝2兾)傪揧晅偣傛丅
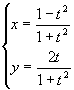 偱昞偝傟傞嬋慄傪丆僐儞僺儏乕僞傪梡偄偰偐偗丅傑偨丆偙偺嬋慄偼墌偱偁傞偙偲傪帵偣丅
偱昞偝傟傞嬋慄傪丆僐儞僺儏乕僞傪梡偄偰偐偗丅傑偨丆偙偺嬋慄偼墌偱偁傞偙偲傪帵偣丅
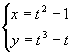 (-2亝t亝2)偱昞偝傟傞嬋慄傪C偲偡傞丅
(-2亝t亝2)偱昞偝傟傞嬋慄傪C偲偡傞丅(1) 僐儞僺儏乕僞傪梡偄偰丆嬋慄C傪偐偗丅
(2) k 偑-6亝k亝6偺斖埻傪摦偔偲偒丆捈慄y=k偲嬋慄C偲偺嫟桳揰偺屄悢偼偳偺傛偆偵曄傢傞偐丆僐儞僺儏乕僞傪梡偄偰挷傋傛丅
(1) r=兤/2(0亝兤亝4兾)
(2) r=log兤(1亝兤亝6兾)
(3) r=e兤/3 (-2兾亝兤亝2兾)
(1) 僐儞僺儏乕僞傪梡偄偰丆嬋慄C傪偐偗丅
(2) b>0 偲偟偰丆b偑戝偒偔側偭偰偄偔偲偒丆墌r=b偲嬋慄C偲偺嫟桳揰偺屄悢偑偳偺傛偆偵曄壔偡傞偐丆僐儞僺儏乕僞傪梡偄偰挷傋傛丅
(1) r=2cos兤丂丂丂(2) r2 sin2兤=2
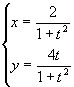 偱昞偝傟傞嬋慄傪C偲偡傞丅
偱昞偝傟傞嬋慄傪C偲偡傞丅 (1) 僐儞僺儏乕僞傪棙梡偄偰丆嬋慄C傪偐偗丅
(2) C偼懭墌偱偁傞偙偲傪帵偣丅
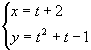 偱昞偝傟傞嬋慄傪偐偗丅
偱昞偝傟傞嬋慄傪偐偗丅