―私の数学散歩道(50)― シンプルな三元四次連立方程式を解いてみたが、それでも大変！
@Author Youichi.Murata @Version1.00;24.Aug.2024
高次方程式を考えているうちに、２～４次の連立方程式の解法に思い至った。思考錯誤で式を立て、たまたま全ての解を求めることができたので紹介する。
―私の数学散歩道(49)― 少し難しい分数関数の積分について
@Author Youichi.Murata @Version1.00;15.Jun.2024
三角関数、無理式や高次式を含む分数関数の積分から何年も遠ざかっていたら、すっかり勘が鈍ってしまった。
取り戻そうとやってみたが、まだまだこれからのよう・・。
―私の数学散歩道(48)― 因数分解と方程式の解法が決め手となる問題について
@Author Youichi.Murata @Version1.00;10.Jun.2023
特別、かつクイズ的な2変数の不定方程式や高次分数関数の積分の可能性の判定には因数分解と方程式をいかにうまく解くかがポイントになる。今回はこのタイプの問題を考えてみた。
―私の数学散歩道(47)―幾分難しい因数分解
@Author Youichi.Murata @Version1.00;10.Jun.2023
微分と積分、式の展開と因数分解など数学には逆算の関係がよく出てきます。
他の逆算の演算と同様、式の展開は機械的にできるが、因数分解はテクニックも必要で
難しくなる。今回は高次式の新作問題を含め考えてみた。
―私の数学散歩道(46)―自然数の累乗和（冪：8から10まで）ほかの因数分解について
@Author Youichi.Murata @Version1.00;26.Nov.2022
各々の計算結果は9～11次の高次式などで 一般的な解法を知らないが知る限りの知識で
チャレンジしたもの。各位のご指導をお願いしたく。
―私の数学散歩道(45)―手計算による自然数の累乗和（冪：1から10まで）の算定について
@Author Youichi.Murata @Version1.00;26.Nov.2022
自然数の累乗和、とくに冪が8,9,10の公式に興味を持ち インタネット等で調べたが難解な
理論が多かった。資料では計算が煩雑すぎ計算ソフトの使用を勧めていたが、高校数学での
方法で敢えて解いてみたもの。
―私の数学散歩道(44)―初等数学第92号「第91号に関連して」について
@Author Youichi.Murata @Version1.00;4.Jun.2022
題記の初等数学第92号に西山先生の下記コメントがあり、興味を覚えたため(1)～(3)の解答を
試み 気付き事項を付け加えてみた。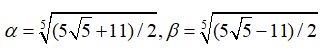
の時 (1) αβを
求めよ。(2) α－β－１ の正、負、or 0 を判定せよ。・・・から
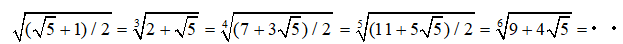などの面白い数列の相等が示した。
―私の数学散歩道(43)―デカルトの葉線からの無理数の相等ほか（関連）
@Author Youichi.Murata @Version1.00;29.Jan.2022
デカルトの葉線の極値を通り対称線に直交するもう一つの交点から117回の無理数の相等を示したが、今回 葉線上の解となる座標を通る場合もOKのケースがあることがわかった。
しかも前者の基本方程式は の値に関わらず同じである。更にデカルトの葉線から離れるが、4次・5次の代数曲線と比較・検討してみた。
―私の数学散歩道(42)―デカルトの葉線からの無理数の相等ほか
@Author Youichi.Murata @Version1.00;30.Jan.2021
デカルトの葉線に興味を持ち 直交座標や極座標での方程式、曲線の対称線、漸近線、その概形、関数の極値などを考えた。極値を通り対称線に直交するもう一つの交点から
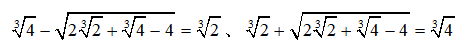という面白い結果が得られたので
紹介する。
―私の数学散歩道(41)―「はやぶさ」の軌道計算に有効な円周率の精度は？・・
@Author Youichi.Murata @Version1.00;30.Jan.2021
去年は「はやぶさ２」の帰還で終わったが、軌道計算には円周率が必要なはずと資料を探していたら「とてつもない数学」に小数点以下15桁のπを使っているよう、とあった。
調べた範囲の円周率公式で何回の計算で上記のπが求められるか当たってみた。
―私の数学散歩道(40)―実数解１個と二次式の平方根３個を持つ無理方程式の解法
@Author Youichi.Murata @Version1.00;29.Aug.2020
今回 偶然見つけた3個の根号の中が２次式で規則性を持つ無理方程式の右辺の２個の無理式を入替え解いてもすべて
１個の実数解を得た。規則性がない同様の無理方程式の場合もこれが成り立つ。勿論、一般的証明ではなくお遊びであるが、
それにしても時間がかかった。
―私の数学散歩道(39)―前回レポから派生する因数分解
@Author Youichi.Murata @Version1.00;29.Aug.2020
前回の数学散歩道(38)の過程で出てきた係数の絶対値がすべて1の式の因数分解に興味を持ち、数列状の多項式や特別な三項式、それらの交項式に最高次数など条件を付し調べたものです。
―私の数学散歩道(38)―二項式（x42 - 1）を因数分解してみよう！
@Author Youichi.Murata @Version1.00;6.Jun.2020
ブルーバックスの「ゆっくり考えよう！ 高校・総合学習の数学」の中にあった二項式
xn-1の因数分解に興味をもった。同書ではn＝30,105の説明と解答があったが、
小生はn=42にチャレンジしたもの。
―私の数学散歩道(37)―かなり面倒な三角方程式
@Author Youichi.Murata @Version1.00;25.Jan.2020
前回の散歩道(36)で三角方程式sinx sin2xsin5x=1/8(0 計算が煩雑で時間もかかったが何とかまとめることができた。
―私の数学散歩道(36)―幾分面倒な三角方程式と覆面算
@Author Youichi.Murata @Version1.00;30.Nov.2019
今回は幾分面倒な自作の三角方程式２題と「初等数学」で興味を持った覆面算にチャレンジしてみました。ほかにうまい解があればご教示ください。
―私の数学散歩道(35)―三角関数（tan 3n° n∈N）の無理数表示を中心にして
@Author Youichi.Murata @Version1.00;31.Aug.2019
既定の30°45°60°に15°18°を加え の三角関数を手計算で求めるのも面白いと思い試みた。この途中で某氏から 等も無理数表示できるという書類を受け取ったが、式が不正確で小数表示してみた結果も一致しない。
角の三等分問題とも絡み、計算不能というのが正しい答えであろう。
―私の数学散歩道(34)―無理方程式
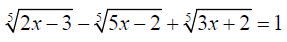の代数学的解法は？
@Author Youichi.Murata @Version1.00;26.Jan.2019
高校では幾つかの平方根や立方根を含むものを扱ったが、４乗根以上のものは皆無であった。このたび題記方程式を考え、その解を導く過程から一般の無理方程式を解く問題点を検討してみた。
―私の数学散歩道(33)―ちょっと面倒な等式の証明
@Author Youichi.Murata @Version1.00;26.Jan.2019
数学Ⅰの入口「式と計算」に立ち返って新作や改作問題等を中心に等式の証明に絡むものを纏めました。問題は幾分捻ってあり、やりがいがあります。余韻を楽しんで下さい。
―私の数学散歩道(32)―自作の未決作問解決への道は？
@Author Youichi.Murata @Version1.00;1.Dec.2018
拙著「私の数学散歩道」で考えた問題の特殊な解（数値例 ｎで表示）は問題なく解けましたが、一般的な解（ｎ，ｋで表示）について今まで幾度か挑戦するも解けません。諸先生のお力で解いていただければ幸いです。
―私の数学散歩道(31)―特別な形の連立方程式について(２)
@Author Youichi.Murata @Version1.00;4.Aug.2018
前回の「私の数学散歩道(29)」と同じ発想でｎ＝４のとき、をｎ＝５に拡大したものです。計算が非常に煩雑で、これが手計算の限界かと感じました。
―私の数学散歩道(30)―幾分難解な三角方程式について(２)
@Author Youichi.Murata @Version1.00;2.Jun.2018
私の数学散歩道(28)の問題(3)を一般の場合に拡張し、その解を複素数ほか2つの方法で求めた。また結果的に数学的帰納法による証明となるが、解の確認も付け加えた。
―私の数学散歩道(29)―特別な形の連立方程式について
@Author Youichi.Murata @Version1.00;2.Jun.2018
「初等数学」83号の課題コメントの中に、ｎ＝4（意味はcf.レポ）の場合 右辺の4係数のみがa～dで与えられた4元4次連立方程式があった。因数分解を用いるくらいで解けるようa～dを決定、その解を求める問題は・・とあり、チャレンジしてみました。
―私の数学散歩道(27)―高階の階差を持つ数列の一般項・漸化式とその和について
@Author Youichi.Murata @Version1.00;30.Jan.2016
何個かの項の数列が与えられその一般項を求めよ、という問題をよく見ます。
階差から数列の規則性を見つけ計算しますが、一般項の証明を要求していないため、それだけ
では一般項が正しいかどうかが気になりました。
そこでSnの成立を数学的帰納法で証明しSn－Sn-1＝an (n≧2，かつa1＝S1 n＝1)
からanの正しさを確認、併せて漸化式を計算しました。類似の問題は探した範囲では見当りませんでしたが、漸化式や和を持つ数列のanは推定でも正しいためでしょう。
数列は等比数列と雑数列を組み合わせ試行錯誤で作成、問題も適宜纏めたものです。
―私の数学散歩道(26)―三角・対数・指数等の各種方程式について
@Author Youichi.Murata @Version1.00;28.Nov.2015
今回下記の4題の方程式を考えます。
（１）は 201年防衛医大の問題を120°＝α，0°＜α＜360°として他にも解がないかを含めて方程式の問題に転化
したものです。これを方程式にするとあまり見たことのない式変形が現われ、興味を覚える解答になりました。
（２）～（４）は自作問題で,とくに（４）で現れた11 次の高次方程式が正の実数解を持たないことを示すのに苦労しました。
微分法では高次導関数が出てきて纏めにくく掲載の通りとしました。
良い解答が見つかればご教示ください。
―私の数学散歩道(25)―1997センター入試（追試験）数学Ⅱ・数学Ｂ 第１問(1)の別解検討
@Author Youichi.Murata @Version1.00;3.Oct.2015
センター試験の過去問を遡って見ていたら下記の問題が気になりました。面白そうで、いくつか別解が見つかる可能性があり挑戦してみたところ、問題の指示に沿った解を含めて下記4つの解を得ました。
また通常答としての最大値、最小値のほかそのときの座標を示すことが多いですが、本問ではその設問がないため追加しその理由を考えてみました。
結論は問題の誘導から考えて計算が煩雑で、時間不足に陥るためと推定しました。
その他の解答があればご教示下さい。
―私の数学散歩道(24)―無理方程式について
@Author Youichi.Murata @Version1.00;6.Jun.2015
題記の方程式と問題B は、［初等数学］第76号掲載の「課題１」(問題Ａ)をヒントに作題したもので、当初の問題の視点を変えて見たものと言える。
―私の数学散歩道(23)―cos20ﾟ,cos40ﾟ,cos80ﾟを解とする数値係数の３次方程式を探る
@Author Youichi.Murata @Version1.00;31.Jan.2015
数学散歩道(20)で正接の角がＡ.Ｐ.をなす角αを求めましたが、今回は余弦の角がＧ.Ｐ.をなす問題を考えてみました。
―私の数学散歩道(22)―少し工夫が要る不等式の証明(2)
―私の数学散歩道(22)―少し工夫が要る不等式の証明追加分
@Author Youichi.Murata @Version1.00;29.Nov.2014
前回同様「数学のいずみ」掲載の柳田五男氏編「初等的な不等式」から興味深く、かつ有名・無名の定理や補助公式を使わず、定石や正攻法を使いある程度高校生が解けると考えた不等式６問を選び解答をつけたものです。
―私の数学散歩道(21)―少し工夫が要る不等式の証明～柳田五夫氏の「初等的な不等式」より～
@Author Youichi.Murata @Version 1.00;9.Aug.2014
「数学のいずみ」の新着情報を見ていたら、「初等的な不等式」に余り見慣れない興味ある不等式がたくさん載っていました。今回はその中から有名・無名の定理や補助公式を使わず、定石や正攻法で高校生が解けると考えた不等式を6 問選び解答をつけたものです。
オリジナルには解答がついている問題もありましたが、小生なりの方法で解答しました。掲載問題は数百題にのぼりＩＭＯ関連等難かしい問題も多いですが、少しずつチャレンジしていきたいと思っています。
―私の数学散歩道(20)―tanα=tan2αtan3αtan4αこの式が成り立つ左辺の角α (0°<α<90°）は？
@Author Youichi.Murata @Version 1.00;25.Jan.2014
数研出版の2013 入試問題集（数学Ⅰ・Ⅱ・A・B／理系）掲載の問題152.
tan10°＝tan20°tan30°tan40°・・・① を示せ。（13 千葉大・理）
を見て何ときれいな式だろう。一つの正接の角が別の三つの正接の角の積で、しかも角がこの順に等差数列をなしています。そこで角が初項α ，公差α の等差数列をなすこのほかに成り立つ角を探してみよう、というのが本稿の主旨です。
―私の数学散歩道(19)―４次関数に放物線（形状）が現れた…の検討について
@Author Youichi.Murata @Version 1.00;30.Nov.2013
今回は問題提起2問を取り上げ、各々検討し課題を提示してみました。
―私の数学散歩道(18)―自作による雑問題5 問とその解答について(2)
@Author Youichi.Murata @Version 1.00;8.Jun.2013
今回は自作による三角関数の証明問題2 題、図形の面積と積分計算の2 題、図形絡みの微分と整数についての1 題の計5 題について問題と解答を作ってみました。
(第１問)の垂線の長さは公式からすぐ出ますが、式の変形で迷いそうです。また別解も面白そうです。(第2 問)は複雑な式に惑わず、置換えや式の扱いに注意が必要です。(第3 問)は3次関数の性質と定数α β の大小関係がポイントです。(第4 問)は直接計算するのが面倒で簡単な積分を求め足掛かりにするのが大切、(第5 問)の(2)は整数解絡みで少し考えさせられます。でははじめましょう。
―私の数学散歩道(17)―自作による雑問題６問とその解答について
@Author Youichi.Murata @Version 1.00;8.Jun.2013
今回は自作による方程式、図形と方程式、無限級数、積分と求積、簡単な積分方程式について問題と解答を作ってみました。(第１問)はガウス記号が入った一次方程式ですが、どう手をつけるかで迷いそうです。(第2 問)は図形の標準問題、(第3 問)は分母が複雑ですがどう部分分数に分解するかが鍵に
なります。(第4 問)はどのように計算するかがポイント、(第5 問)は求積の問題ですが、計算が面倒です。最後の(第6 問)は概ね計算問題ですが、計算ミスをしそうです。落ち着いて行きましょう。
―私の数学散歩道(16)―自作の（連立）方程式とその解法について
@Author Youichi.Murata @Version 1.00;26.Jan.2013
本稿では余り見ない幾つかの方程式とその応用問題を考え、それらの解法をまとめてみました。特別な形の三元三次連立方程式、平方根・立方根を含む連立方程式、log(sin x)とlog(sin y) ,あるいはlog(log u)を含む方程式、前提条件なしにtan(π/20)を計算で求める問題、一次式に指数関数が混じった連立方程式です。
―私の数学散歩道(15)―数式等の英語での読みについて（その２）
@Author Youichi.Murata @Version 1.00;1.Dec.2012
毎日のように見慣れている数式等ですが、これらを英文で表現したらどうなるか考えてみました｡今回は主に数研出版2011～12 入試問題集数学Ⅰ・Ⅱ・A・B の領域から数と式、関数と方程式・不等式、式と証明、場合の数、
三角比・三角関数、指数関数・対数関数とそれらの応用の分野の公式や代表的な数式、方程
式等を選び纏めたものです。
―私の数学散歩道(14)―「方程式が解を持たない」ことを利用して解く問題の作問について
@Author Youichi.Murata @Version 1.00;1.Dec.2012
今回は「方程式の解が存在しない」ことを示すことで解ける問題を考えまとめてみました。
―私の数学散歩道(13)―数式等の英語での読みについて（その１）
@Author Youichi.Murata @Version 1.00;4.Aug.2012
毎日のように見慣れている数式等ですが、これらを英文で表現したらどうなるか考えてみました｡幸い稿末表示の良いテキストが見つかり、英語が好きなこともあって不明な表現は真似るなどしてチャレンジしたわけです。
―私の数学散歩道(12)―連立方程式を解く楽しみ～ラグランジュの未定乗数法：多変数関数の極値の算定について～
@Author Youichi.Murata @Version 1.00;4.Aug.2012
周知の通り多変数関数の極値は偏微分で求められます。その際偏微導関数や偏微係数、極値決定のための行列式の計算等が煩雑です。その点ラグランジュの未定乗数法ではとくに極値の存在がわかっている場合､計算が連立方程式の解法に帰せられ親しみやすく今般、方程式の解法を楽しみながら、例題３題を未定乗数法に絞って纏めてみました。
―私の数学散歩道(11)―ピアーズ・フォスター 簡約積分表の公式の証明(3)
@Author Youichi.Murata @Version 1.00;2.Jun.2012
今回は「指数関数及びその他の関数を含む式」で、これをもって本シリーズの最後としたい。
見なれない公式も多いが、これにより難関大学を含め入試等に出てくる指数関数を含む積分の
計算に殆ど対応できると思う。解法のポイントは置換積分と部分積分が主であるが、結構計算
が面倒なものもある。
―私の数学散歩道(10)―ピアーズ・フォスター 簡約積分表の公式の証明(2)
@Author Youichi.Murata @Version 1.00;28.Jan.2012
今回は「三角関数を含む式」とし266.から389.の公式より適宜選んで証明をつけた。
部分積分の公式にこれらを組み合わせることで、実際入試等に出てくる三角関数を含む積分の計算に
殆ど対応でき、また公式によっては積分の練習問題としても使えると思う。
―私の数学散歩道(9)―ピアーズ・フォスター 簡約積分表の公式の証明
@Author Youichi.Murata @Version 1.00;26.Nov.2011
積分の計算は数学Ⅲの一つの核をなすもので、題記の積分表を見て役立ちそうな分野の
公式を証明しておくと授業にも有用と考え、取り上げることにした。
今回は「対数関数を含む式」とし442 から460 のすべての公式の証明をつけた。
知らない公式も多いが、これにより難関大学を含め入試等に出てくる対数関数を含む積
分の計算に殆ど対応できると思う。
―私の数学散歩道(8)―特殊な高次の連立方程式
― 遊び心の観点から別解を探る―
@Author Youichi.Murata @Version 1.00;6.Aug.2011
今回は自作の１．三元四次連立方程式を考え、それに途中から遊び心で４個の
異なる解を与え、また別の2．三元二次連立方程式では３個の別解を示しました。
―私の数学散歩道(7)―ある大学入試問題への9個のアプローチ
― ある大学入試問題への９個のアプローチ―
@Author Youichi.Murata @Version 1.00;13.Dec.2010
楕円上の点における接線がつくる切片が作る線分の長さについての問題に対して、いくらか共通する解法を含むものの９個の別解を調べてみました。
これら以外の別解を見つけた方は、ご教示願えれば幸甚です。
―私の数学散歩道(6)―たかが因数分解、されど因数分解
@Author Youichi.Murata @Version 1.00;11.Feb.2011
高校数学を学ぶに当たり、因数分解の必要によく迫られる。
式と計算の分野は言うに及ばず方程式や不等式の解法、等式や不等式の証明など枚挙に暇がない。数学Ⅰで勉強する共通因数の括り出し、因数定理による因数の探索、一文字や最低次の文字について整理、公式の直接利用などだけでは対応できない例を考え、あるいは探して自分なりのやり方で解いてみた。
―私の数学散歩道(5)―別解探求による問題演習と学力アップ
― ある大学入試問題への９個のアプローチ―
@Author Youichi.Murata @Version 1.00;13.Dec.2010
学力がつき余裕ができると「別解がないか」、と考えるのは自然のように思います。
すべての問題が別解を持つものでありませんが、常にこのような眼で見ていると多面的な
方向から一つの問題を攻めるフレキシブルな頭脳ができてきます。
私の数学散歩道 (4)
～積分を電卓と筆算で計算しよう！～
@Author Youichi.Murata @Version 1.00;15.Sep.2006
「数学散歩道シリーズ」第４弾。積分計算を考え方や途中の計算もいろいろあると思うが、
つれづれなるままに計算し、たいへん長い「私の数学散歩道」となった。最後までご覧いただければ幸いである。
私の数学散歩道 (3)
～新作問題と解答：等式、方程式、不等式篇～
@Author Youichi.Murata @Version 1.00;15.Sep.2006
自作の方程式、不等式に関する新作問題。「数学散歩道シリーズ」第３弾。
私の数学散歩道 (2)
～新作問題と解答：三角関数との融合を視点に～
@Author Youichi.Murata @Version 1.00;15.Jul.2006
三角関数の融合問題の新作を紹介。好評の「数学散歩道シリーズ」第２弾。
私の数学散歩道
－関数 fn(x)=sinnx + cosnxの変域についての６個の証明と fn(x) の特徴、数学上の美
@Author Youichi.Murata @Version 1.00;19.Mar.2006
関数 fn(x)=sinnx + cosnxの変域について，幾通りもの証明を通してfn(x) が持つ特徴を考察するとともに，その数学的美しさに触れる。
