Drone-Schema による２次関数の最大・最小の小手技
@Author Fuminori.Nakamura @Version 1.00;25.Nov.2023
定義域や放物線が動く場合の最大・最小問題をリニューアルしました。指導案の「メイクる数学」、まとめの配布資料Mathtemplate、そして授業記録である小手技。３つのシリーズのコラボで授業は展開します。また、最大値と最小値を変数で場合分けする場合、表として簡潔に答をまとめる方法を提案しています。
ベクトルの始点と視点の小手技
@Author Fuminori.Nakamura @Version 1.00;10.Jun.2023
ベクトル計算は、オートマチックカリキュレートの傾向がありますが、始点を変えると思
考的な考察もできるようになります。さらに、視点、支点を工夫してベクトルの面白味を引
き出してみましょう。応用として、スチュワートの定理、オイラー線、チャップルの定理を
扱っています。
垂線ベクトルの小手技
@Author Fuminori.Nakamura @Version 1.00;10.Jun.2023
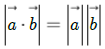は一見するとスカラー量の絶対値の性質と同じですが、ベクトルではシュワ
ルツの不等式の等号成立であり、２つのベクトルの平行条件を表しています。これを利用し
て、垂線ベクトル(造語)を考え、平面上での点と直線の距離、空間内での点と平面の距離を
ヘッセの標準形により導きます。さらに点が平面によって分けられる空間の正領域、負領域
にあるための条件を示し、空間に図形をレイアウトしてみましょう。
正射影ベクトルの小手技
@Author Fuminori.Nakamura @Version 1.00;10.Jun.2023
教科書では内積(dot-product)は図形的な意味から定義されているわけではなく、余弦定
理のベクトル表現とか、垂直条件などに読み替えられてしまいます。これを正射影ベクトル
で考えると内積の見方はずいぶん変わり、ベクトルの概念が豊かになるのです。
例として、三角形の五心の位置ベクトルを正射影ベクトルを利用することで統一した解
法にしてみましょう。また、空間の異なる３点により定まる平面に垂直なベクトル(法線ベ
クトル)を、垂直条件を用いないで求めてみましょう。
格子点の個数の小手技
@Author Fuminori.Nakamura @Version 1.00;27.Aug.2022
格子点の個数を題材に、多面的に試行を広げてみたレポートです。１つの問題と対峙する際に、どのツールを用いて解くかを考えるという数学の楽しみが感じられます。
４つの和集合の個数の小手技
@Author Fuminori.Nakamura @Version 1.00;5.Jun.2021
1000以下の素数の個数は，エラトステネスの篩の原理をプログラムして計算すると168個あります。これを「250以下であることを示せ」，このように概数にすると，大学の入試問題になります(2021年度一橋大学)。その解法を4つの和集合の個数，包除の原理，オイラーの関数と広げ，いつもの4人が「数学のよさとは何か」を考えながら探っていきます。
不定方程式の解の小手技
@Author Fuminori.Nakamura @Version 1.00;23.Jan.2021
2元1次(ベズー)不定方程式の特殊解は方程式の係数や定数項を小さくすることでユークリッドの互除法を用いないで求めることができます。その変形の保障となっているのは互除法と合同式の考え方です。今回は，大学入学共通テストの誘導問題例を作成し，ナビゲーターの太郎と花子(タロハナ問題と命名しました)に変わっていつもの4人の乱打戦でお楽しみください。
さいころの目の最大・最小の小手技
@Author Fuminori.Nakamura @Version 1.00;23.Jan.2021
さいころの目の最大値が4である確率は，最大値4以下から最大値3以下を除いて求めるのが通常の解法です。これを最大値4以上から最大値5以上を除いて求めることは誤りなのでしょうか。そもそも「以上・以下」という技法で求めることはどうなのでしょう。このことを，カルノー図を用いていつもの4人が議論します。
組立除法の小手技
@Author Fuminori.Nakamura @Version 1.00;18.Jul.2020
高次方程式の近似解を求めるために考案されたHorner法の1次式での除算を組立除法といいます。一般的な方程式の解法以外に，関数の平行移動，接線の方程式，恒等式，微分係数などでとても便利なItemとして様々な分野で活用することができます。ここでは触れませんが，定積分やn進法にも応用可能です。必須のItemとして，携帯してみてはどうでしょうか。
放物線の接線の小手技
@Author Fuminori.Nakamura @Version 1.00;11.Jun.2020
カヴァリエリのは，微分積分の概念を発見したニュートンやライプニッツと同時体の数学者です。彼が提唱したカヴァリエリの原理は図形求積としては直感的・観念的なものですが，そこから思考を進める入口としては素晴らしい概念です。本文では，放物線を一定方向に切り分け整形しなおすことで微分，判別式のツールを用いることなく放物線の接線を求めています。
スラック変数による重複組合せの小手技
@Author Fuminori.Nakamura @Version 1.00;6.Jun.2020
組合せが，x+y+z?10 のように不等式で与えられる場合，その個数を求めるには場合分けが必要になる。これを線形計画法で利用するスラック(slack)変数を用意すと，不等式を等式に変えることができ，簡単に求められる。重複組合せの個数についてもスラック変数で考察を試みる。
メネラウス・チェバの小手技
@Author Fuminori.Nakamura @Version 1.00;6.Jun.2020
定理を発見した2人の数学者メネラウスとチェバは1600年ほどの時代の隔たりはある。しかし「三角形を切る」ということでは同じものである。三角形の点を周遊しながら一周するとみて，パズル感覚で定理の理解をしよう。さらに，空間内の四面体でもメネラウスの定理は成立することを示す。
3点を通る曲線の小手技
@Author Fuminori.Nakamura @Version 1.00;6.Jun.2020
3点を通る放物線および3点を通る円の方程式は「2曲線の交点を通る曲線」の性質を利用すると統一した解法になる。陰関数を用いると複数の曲線を一般形で表すことが可能になる。したがって，二次曲線と考えてしまえば，円も放物線も同じに扱うことが可能である。
微分係数の定義の小手技
@Author Fuminori.Nakamura @Version 1.00;6.Jun.2020
微分係数は2つの定義が用意されているが，それぞれどういう場面で使うのだろう。「極限から微分係数を求める」のではなく，「微分係数から極限を求める」と考えることで，極限の問題は，単純な微分係数の問題に変わってしまう。それはロピタルの定理の簡易バージョンとみなすこともできる。
漸化式の平衡値の小手技～漸化式の項をShareしよう
@Author Fuminori.Nakamura @Version 1.00;28.Nov.2015
非同次式(非斉次式)の一般解は，その特殊解と同次式の一般解の和として得られる。
本文の内容は一言でこのように表現される。ここで非同次式の特殊解は特性方程式の解として得られる。また，同次式の多くは等比数列の一般項である。ただ，原理としてはそうであるが，本文はそんな大げさな性質を大上段に構えて論じてい
るわけではない。いたって単純であり，「項の値をシェアする」操作で漸化式の一般項を求めてみようという内容である。
特性方程式は，漸化式の一般解の解法のキーワードとして自然に用いられようになった。しかし特性方程式や特殊解(特性根)という用語の定義がないまま，使えば求められるという極めてマニュアル的な説明で用いられる。何か「特性」は「特別」なものとして捉えられ，そういう特別なテクニックをかざせば解決できるという発想はどうなのだろう。
補角から眺めた三角比の小手技
@Author Fuminori.Nakamura @Version 1.00;31.Jan.2015
角の二等分線の問題から始まり、四角形から三角形へのトランスフォームにまで話題が発展してしまいました。
遊び心から始めたトランスフォーメーション(変換ではなく変形)解法の思いがけない副産物です。
整数の下二桁の値のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;3.Aug.2013
過去の学習指導要領の元での教科書にはオイラーやフェルマーの定理を載っているわけではない。しかし、その当時の大学受験の問題集や参考書では、入試で出題されることもあり、当然の如く解説されていたし、またそれはガウスのような大数学者の業績に触れることのできる嬉しい機会でもあった。数理重視の切り札の一つとして復活した整数の性質は、随分昔に扱われたものであり、現場で指導したことのない教師が大多数かもしれない。その指導法もまだまだ未開拓といえる。この古くて新しい素晴らしい分野に対し、本研究会においても多くの先生方の指導実践とそのあいのりを望みたいと思う。
多面体定理のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;10.Jun.2013
定理の証明については正多面体の面、辺、頂点の数を調べるだけで「推測」するものであり、正多面体が五種類しかないことの証明も割愛されている(研究としては載っているが)。「仏造って魂入れず」である。面、辺、点の数にどうしてこのような関係が成立するかを正多面体で調べ、そこから性質を予想・組立て、そして証明する道筋こそが、活用力の育成であり、数学のよさの認識であるはずなのだが、その証明がまったく触れられていないのである。そこで、今回の小手技は、これを盛り込むことにした。
３次式で割った余りの小手技
@Author Fuminori.Nakamura @Version 1.00;6.Aug.2011
今回の小手技は、「翻訳のタイミング」をテーマにしています。この分野に限らず、条件文の定式化は、どの段階で、どの部分まで、どのように翻訳するかで大きく解法の方針が異なってきます。
三角関数の解法の小手技
@Author Fuminori.Nakamura @Version 1.00;11.Jun.2011
向かい合う辺と角の組を最良のカップルと見て残りのパートナー探しを試みる、対辺・対角を意識しながら三角形の解法に臨むという方針設定の小手技。
必要十分条件の小手技
@Author Fuminori.Nakamura @Version 1.00;28.Jun.2010
必要十分条件は集合の包含関係に置き換えられる。あとがきのあとがきでは命題や逆、対偶についての考察が為されています。
集合の要素の個数の小手技
@Author Fuminori.Nakamura @Version 1.00;28.Jun.2010
集合の要素の個数をベン図ではなく、カルノー的分類法で考えていくと…。
必要十分条件の小手技
@Author Fuminori.Nakamura @Version 1.00;28.Jun.2010
必要十分条件は集合の包含関係に置き換えられる。あとがきのあとがきでは命題や逆、対偶についての考察が為されています。
事象の排反と独立の小手技
@Author Fuminori.Nakamura @Version 1.00;28.Jun.2010
排反と独立の違いは何でしょう。そんなの関係ねぇ関係を整理していきます。
背理法と対偶による証明の小手技
@Author Fuminori.Nakamura @Version 1.00;28.Jun.2010
背理法と対偶による証明をいつものメンツのやり取りの中から考えていきます。あとがきには、真理表による論理の説明や対偶の導入に関する面白い例、直接証明・対偶法・背理法の証明の比較なども記載されています。
斜交座標系のちょっとした小手技Ⅲ
@Author Fuminori.Nakamura @Version 1.00;29.Nov.2008
バランスメソッドは空間でも成り立つのでしょうか。空間と平面の関係から見つめていきます。
円の接線と極線の小手技
@Author Fuminori.Nakamura @Version 1.00;14.Aug.2008
円の接線を求めるときによく見られる間違えを誤認誘導として接線へ導いていく流れとともに、「ではその間違った直線は何であるか」まで示されています。
斜交座標系のちょっとした小手技
斜交座標系のちょっとした小手技Ⅱ
@Author Fuminori.Nakamura @Version 1.00;14.Aug.2008
三角形とベクトルには斜交座標がよく馴染むのがわかります。メネラウス型の三角形へのアプローチも興味深いものとなっています。
解の配置問題のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;11.Jun.2008
解の配置問題（解の存在範囲）はなかなか難しい問題です。しかし「てんじく蝶」が解答へ導いてくれます。
出会いの確率の小手技
@Author Fuminori.Nakamura @Version 1.00;2.Feb.2008
最短経路の確率の問題を「同様に確からしい」と絡めて分析する。
ランダムウォークの確率の小手技
@Author Fuminori.Nakamura @Version 1.00;2.Feb.2008
酔歩の確率をカタラン数とからめて分析する。
曲線外から引いたグラフの接線の小手技
@Author Fuminori.Nakamura @Version 1.00;23.May.2007
曲線外から引いた接線の求め方をスマートに求めよう。
f(x)/xのグラフの接線の小手技
@Author Fuminori.Nakamura @Version 1.00;1.Aug.2006
勾配関数とその反転関数の性質をもとに，グラフの概形を探ることができる。さらに00のイメージ化を考えよう。
じゃんけんの勝敗確率の小手技
@Author Fuminori.Nakamura @Version 1.00;6.Aug.2004
人数が増えれば増えるほどじゃんけんで一人の勝者を決めるのに時間がかかります。最後に一人の勝者が決定するまでの期待値(平均)を考えてみましょう。
辞書式配列のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;27.Nov.2004
場合わけが面倒な辞書式配列に関する問題を簡単な方法で解きます。目からうろこが落ちるような，そんな解法を紹介。
ap計算のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;5.Jun.2004
対数に関するちょっとした公式，だけど使い勝手のよい味のある公式を用いた計算方法を取り上げる。
放物線の共通接線のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;31.Jan.2004
２つの放物線の共通接線の方程式をもとめる裏技を紹介。開き(2次の項の係数)の絶対値が等しい放物線のグラフだけでなく，開きが違う場合についての共通接線についても取り上げる。
関数の極限のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;14.Jun.2003
無限小を調べるアイテム，Maclaurin展開，Maclaurin級数での近似，ロピタルの定理，そしてランダウのオーによる漸近展開などのアイテムを使って関数の極限に関する問題を解いてみよう。
複素数の割り算のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;1.Feb.2002
複素数のわり算について，直交座標平面，斜交座標平面，複素数平面の３つの平面の比較から迫る。
３次関数の標準形の小手技
@Author Fuminori.Nakamura @Version 1.00;30.Nov.2002
変曲点における接線の傾きは、２極点を結ぶ直線の傾きの3/2倍である。この事実から３次関数の標準形について考える。
平行性変形でのベクトルの小手技
@Author Fuminori.Nakamura @Version 1.00;30.Nov.2002
初等幾何における代表的な定理「メネラウスの定理」。そこから派生する様々な定理。この定理の性質をベクトルで読み替えれば、ベクトルの一次独立や共線問題、共点問題が簡単に片付けられてしまうことが分かります。
指数と対数の関係のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;3.Aug.2002
指数とは何者なのでしょう？ 対数の便利性から指数の基本的な性質をもっと見直す必要があるのではないだろうか。
三角関数の合成のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;11.Jun.2002
三角比を円関数としての定義し，三角関数をcosから導入する。cosから導入することで，合成の公式が自然に導かれる。
剰余の定理のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;15.Jun.2002
条件を変形することで余りを作り出すという直接的な解法を用いて剰余定理に関する問題を解いてみましょう。また「数文・和文翻訳」で問題の意味を数学言語で解釈し直しましょう。
正弦定理のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;2.Feb.2002
正弦定理を「弦の長さの比は円周角の正弦の比に等しい」ととらえてみましょう。こうした場合，三角形ＡＢＣにおいては「ａ：ｂ：ｃ＝sinＡ：sinＢ：sinＣ」と表現する方が正弦の本質を表していると考えられる。
数学的帰納法のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;2.Feb.2002
数学的帰納法には、いろいろなパターンが考えられますが，いったいその本質はどこにあるのでしょう。具体例をもとに数学的帰納法の本質に迫ります。
コーシーの不等式のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;1.Nov.2001
最大・最小問題を始めとして多岐の分野で活躍する「コーシーの不等式」。相加・相乗平均では単純に変数を増やしていっても，次元として無限に対応していく。このコーシーの不等式にスポットを当てて見ましょう。
絶対不等式のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;1.Nov.2001
等式に恒等式と方程式の２種類があるのと同様に，不等式にも条件不等式と絶対不等式があります。絶対不等式の中で一番エライ不等式ってなんだろう。
不等式の拡張のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;1.Nov.2001
授業では扱いにくい不等式の証明。絶対不等式のコーシーの不等式，チェビシェフの不等式を変数の個数(次元)で拡張していきましょう。
楕円と直線の関係のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;16.Jun.2001
楕円に関する問題はその補助円を考え，円特有の性質を使えば簡単に求めらることができます。楕円に関する様々な問題を補助円を用いて考えてみましょう。
放物線で囲まれる面積のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;16.Jun.2001
図形を変換することによって，2つの図形で囲まれる部分の面積を簡単に計算することができます。
位置ベクトルの始点の小手技
@Author Fuminori.Nakamura @Version 1.00;16.Jun.2001
位置ベクトルに関するメネラウス型の問題を，各頂点におもりを加えるという単純な操作で解いて見ましょう．計算式をはぶいて，バランスの美しさを楽しんでください．
切頭円柱の体積の小手技
@Author Fuminori.Nakamura @Version 1.00;2.Dec.2000
切頭円柱はスライスの仕方によって，様々な図形に切り分けられ，そこから体積の指導のいろいろな場面がフィードバックできます。
放物線の切片形の小手技
@Author Fuminori.Nakamura @Version 1.00;2.Dec.2000
２次関数の決定問題を解く問題の中では，２次関数の三態を使い分けます。この中でも特に，３点を通る問題についてｘ座標の意味に拘ってみましょう。
対数による桁数問題の小手技
@Author Fuminori.Nakamura @Version 1.00;2.Dec.2000
桁数問題のうちでも「最高位の数は何か」，「小数第何位に初めて０以外のどんな数が現われるか」といった問題を考えてみよう。
集合による人数計算の小手技
@Author Fuminori.Nakamura @Version 1.00;2.Dec.2000
集合における人数計算の問題をカードを使って考えてみましょう。
等差数列のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;5.Aug.2000
等差数列がnの１次式で表されるということに注目し，“公差”を中心とした等差数列の指導を考える。
四角形の重心のちょっとした誤手技
@Author Fuminori.Nakamura @Version 1.00;10.Mar.2000
四角形の重心はどうやって求めるのか。バランスメソッドを用いて重心について考える。
階差数列のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;4.Dec.1999
一般項がどうなるのか与えておいて階差数列を導入。階差数列の指導法を別な観点から考える。
部分分数分解のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;4.Dec.1999
部分分数に分解するときに，分子に出てくる数はどうやって出すの？ カードゲームのような感覚で，部分分数への分解を工夫してみよう。
組合せのちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;4.Dec.1999
男３人，女２人の５人の中から２人選ぶとき，少なくとも１人女子が含まれる場合の数．複数選ぶ場合において重複なく数える方法について考える．
∑ｋpの計算のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;4.Dec.1999
式を変形することで数列のべき和の問題を簡単に考えていく．整式の割り算で商と余りを求めるホーナー法で式変形もラクラク．
剰余類のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;5.Jun.1999
ｍ(２≦ｍ≦ｋ)の倍数であるかどうかを示すのに，剰余系を考えるのではなく，連続するｋ個の整数の積はｋ！で割りきれる性質を利用する。
点と直線の距離のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;5.Jun.1999
点と直線の距離の公式を，三角比のもつ性質が座標上でどう表現されるかという，その結びつきから指導する。
正弦・余弦定理のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;16.Jan.1999
三角形を解く問題において解法の仕方の問題点はないのか? 正弦定理＋余弦定理＝加法定理？ 第１余弦定理をkey-wordとした，スムーズな流れの指導の組立てを考えます。
群数列のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;1.Nov.1998
原数列が等差数列の場合における仕切りの入れ方と，群数列との関係を考えます。
隣接二項漸化式のちょっとした小手技2
@Author Fuminori.Nakamura @Version 1.00;1.Nov.1998
隣接二項漸化式を特性方程式を発展させて解法するときの，ちょっとした小手技を考えます。
数列{n・2n-1}の和のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;1.Nov.1998
等差・等比数列の積で作られるmarriage数列。その和を求めるための指導法を考える。
絶対値不等式のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;1.Aug.1998
絶対値の入った不等式｜x－1｜≧2x＋3を x－1≦－(2x＋3)，2x＋3≦x－1 と直接解いていいの？ そんな「まなぶ法」はどこまで，認められるでしょうか。
隣接二項漸化式のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;1.Aug.1998
「バランスをとる」ことを大事にして，ｎ次式を含む二項漸化式を解いてみよう。
実数条件のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;1.Aug.1998
判別式を使った問題を例に，実数条件についてのちょっとした指導法を考える。
二項係数のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;1.Aug.1998
現教育課程の中におけるオプション分野にコアを調達するのはなかなか大変。そんなとき，さり気なくものぐさにエッセンスだけを提供することも必要。
二次関数の最大最小問題のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;1.Aug.1998
2次関数のグラフの対称性を利用した最大最小問題の解法。発想を転換して，ちょっと視線を変えてとらえてみよう。
二次不等式の解のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.00;1.Aug.1998
水平線を飛ぶかもめのイメージをもとに，2次不等式の解に挑戦。
２次方程式の解のちょっとした小手技
@Author Fuminori.Nakamura @Version 1.10;20.Jun.1998
複素係数をもつ2次方程式に解の公式は使えるの？解と係数の関係は？好評の小手技シリーズ続編。
複素数平面のちょっとした小手業
@Author Fuminori.Nakamura @Version 1.00;10.Mar.1998
複素数計算における効率的な式の整理法，複素平面上における大局的図形概念のイメージ法など，日常の授業における指導法を少し。
数列のちょつとした小手業
@Author Fuminori.Nakamura @Version 1.00;28.Oct.1996
生徒と、そして黒板との格闘との毎日である授業は、時として、苦し紛れの小技を生み出すこともあります。数列に関するそんな話題を少し。
